|
Question 986656: In my Geometry Book it says line GH has endpoints G(-3,2) and H(3,-2)
The question says find GH to the nearest tenth?
I don't understand how to do it please help me
Found 3 solutions by stanbon, mananth, josgarithmetic:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! In my Geometry Book it says line GH has endpoints G(-3,2) and H(3,-2)
The question says find GH to the nearest tenth?
-----
Formula for distance:: D = sqrt[(change in x)^2+(change in y)^2]
-----
Your Problem:
-----
D = sqrt[(3--3)^2 +(2--2)^2]
-----
D = sqrt[6^2 + 4^2]
-----
D = sqrt(36+16)
----
D = sqrt(52)
-----
D = sqrt(4*13)
-----
D = 2sqrt(13)
----------------
Cheers,
stan H.
------------
Answer by mananth(16946)  (Show Source):
Answer by josgarithmetic(39625) (Show Source):
You can put this solution on YOUR website! G and H form the hypotenuse of either of two right triangles. Look at the two points on a cartesian system. The third point may be either (-3,-2), or alternatively (3,2). Either choice, G, and H, and either of the third point form a RIGHT TRIANGLE. You can use Pythagorean Theorem formula to find length GH.
Taking the third point as T(-3,-2), your triangle has legs of lengths 4 and 6; look at the placements and coordinates of the points on your cartesian system for the plotted T, G, and H. The hypotenuse GH will be  .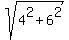
Look in your book if you want to see a derivation of the Distance Formula. It is essentially a form of the Pythagorean Theorem.
|
|
|
| |
