Question 982784: the sides of a triangle are along the lines x-2y=0, 5x-2y=8 and 3x+2y=24. Find the equation of the circle circumscribed about the triangle.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The center of the circle circumscribed about the triangle is at equal distances from all three vertices of the triangle.

A point at equal distance from two vertices must be on the perpendicular bisector of the side connecting those two vertices.

The perpendicular bisector of a segment
is perpendicular and
goes through the midpoint of that segment.
The plan is:
1) find the coordinates of the vertices;
2) find the equations of the perpendicular bisectors of the sides (at least two of them),
and for that we need
a) the slopes of the sides (e.g the slope of AB, 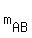 ), ),
b) the coordinates of the midpoints of the sides, and
c) the slopes of the perpendicular bisectors (calculated as the inverse reciprocals of the slopes of the sides);
3) find where the center of the circle (the point where those perpendicular bisectors intersect) 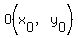 ; ;
4) find 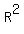 , the square of the radius of the circle (the distance from the center to a vertex), and finally , the square of the radius of the circle (the distance from the center to a vertex), and finally
5) write the equation of the circle as 
1) find the coordinates of the vertices
 ---> --->
 ---> --->
 ---> --->
2a) find the slopes of the sides
side  : :  ---> ---> , so , so 
side  : :  ---> ---> , so , so 
b) find the coordinates of the midpoints of the sides
for side  , we find midpoint , we find midpoint 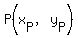 : :


for side  , we find midpoint , we find midpoint 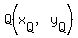 : :


2c) find the slopes of the perpendicular bisectors
for side  , we find the slope of , we find the slope of 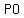 : :

for side  , we find the slope of , we find the slope of  : :

2) find the equations of the perpendicular bisectors of the sides
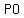 goes through goes through 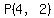 , with slope , with slope  , ,
so its equation is
 ---> ---> ---> ---> , ,
 goes through goes through 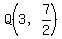 , with slope , with slope  ; ;
so its equation is
 ---> ---> ---> ---> ---> --->
3) find where the center of the circle (the point where those perpendicular bisectors intersect) 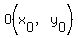 : :
 ---> --->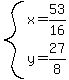
So the center is 
4) find  : :
 so so 

5) write the equation of the circle as 

|
|
|