SOLUTION: The sides of a triangle are on the lines 3x-y-5=0, x+3y-1=0 and x-3y+7=0. Find the equation of the circle inscribed in the triangle.

Algebra ->  Circles -> SOLUTION: The sides of a triangle are on the lines 3x-y-5=0, x+3y-1=0 and x-3y+7=0. Find the equation of the circle inscribed in the triangle.      Log On


   

Question 982783: The sides of a triangle are on the lines 3x-y-5=0, x+3y-1=0 and x-3y+7=0. Find the equation of the circle inscribed in the triangle.
Answer by anand429(138) About Me  (Show Source):
You can put this solution on YOUR website!
Let the centre be (x,y),
The distance of centre from all three sides will be equal to radius.
So, for first two sides,
%283x-y-5%29%2F%283%5E2%2B%28-1%5E2%29%29+=+%28x%2B3y-1%29%2F%281%5E2%2B3%5E2%29
i.e. x-2y-2+=+0------ (i)
And for 2nd and 3rd sides,
%28x%2B3y-1%29%2F%281%5E2%2B3%5E2%29+=++%28x-3y%2B7%29%2F%281%5E2%2B3%5E2%29
i.e. 6y=6
=> y=1----- (ii)
Putting in (i), we get, x=4
So, centre of circle is (4,1)
Now distance of centre from 2nd side = 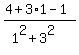%284%2B3%2A1-1%29%2F%281%5E2%2B3%5E2%29 = 3/5
So, equation of circle is,
%28x-4%29%5E2+%2B+%28y-1%29%5E2+=+%283%2F5%29%5E2