Question 969255: Write the equation of the circle satisfying the given condition.
Radius of 2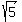 , tangent to y=2x and passing through (3,-4)
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Write the equation of the circle satisfying the given condition.
Radius of  , tangent to y = 2x and passing through (3,-4)
===============
The center has to be on the line parallel to y = 2x and  units from the line.
Find the line's equation:
y = 2x has a slope of 2 and passes thru (0,0)
A line perpendicular to it (RS) thru (0,0) is y = -x/2
A point on the line RS sqrt(20) from (0,0) is the intersection of a circle centered at (0,0) with r = sqrt(20)
--> x^2 + y^2 = 20
y = -x/2
x^2 + x^2/4 = 20
x = 4 (Ignore the x = -4 in Q2, (3,-4) is in Q4)
--> (4,-2)
The center of the circle is on a line thru (4,-2) with m = 2 (parallel to y = 2x)
y+2 = 2(x-4) = 2x - 8
y = 2x - 10
----
Find the point(s) sqrt(20) from (3,-4) on the line y = 2x - 10
It's the intersections of a circle centered at (3,-4) r = sqrt(20)
---
Sub for y
x = 5 --> center @ (5,0) -->  ** Circle #1
----
x = 1 --> center @ (1,-8) -->  ** Circle #2
=============================
There must be an easier way to do this, but I don't know of one.
|
|
|
