SOLUTION: write the equation of the circle satisfying the given condition. Having a radius of {{{ sqrt( 85 ) }}} and passing through (5,9) and (1,-7)

Algebra ->  Circles -> SOLUTION: write the equation of the circle satisfying the given condition. Having a radius of {{{ sqrt( 85 ) }}} and passing through (5,9) and (1,-7)      Log On


   

Question 969254: write the equation of the circle satisfying the given condition.
Having a radius of 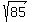+sqrt%28+85+%29+ and passing through (5,9) and (1,-7)
Answer by anand429(138) About Me  (Show Source):
You can put this solution on YOUR website!
Slope of line (or say chord) joining the two points on circumference
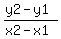
= %28y2-y1%29%2F%28x2-x1%29
= %28-7-9%29%2F%281-5%29
= 4
So, slope of perpendicular bisector of this chord
=-1%2F4 (For perpendicular lines, product of slopes = -1)
So let the equation of perpendicular bisector of this chord(which shall pass through center of circle) be given by
y=+%28-1%2F4%29x%2Bc -(i) (slope-intercept form of a line)
Now mid point of the chord is given by
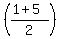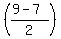
%28%281%2B5%29%2F2%29,%28%289-7%29%2F2%29
i.e.(3,1)
Since this should lie on the line given by eqn (i)above,
So, 1=%28-1%2F4%29%2A3%2Bc
i.e. c=7%2F4
So eqn of perpendicular bisector passing through center becomes
y=+%28-1%2F4%29x%2B7%2F4
or, x=7-4y
Taking center as (7-4y,y), Its distance from both circumferential points is given by radii
So, for point (5,9)
%287-4y-5%29%5E2%2B%28y-9%29%5E2+=+85 (Using Distance formula)
i.e. 17y%5E2%2B34y+=0
i.e. y=0+or+2
So, x=+7+or+-1
There will be two required circles with centers at (7,0) and (-1,2) and radius sqrt(85)
So, the equation of cirles be given by:
%28x-7%29%5E2%2B%28y-0%29%5E2=85 and %28x%2B1%29%5E2%2B%28y-2%29%5E2=85
Simplify, if you want.