Question 958999: A circle has its center at (6, 7) and goes through the point (1, 4). A second circle is tangent to the first circle at the point (1, 4) and has the same area.
What are the possible coordinates for the center of the second circle? Show your work or explain how you found your answer.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first circle is,
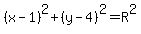
Find R using the point,
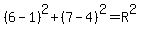


So,
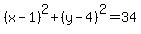
The second circle has the same radius so its equation is,
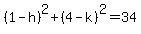
where (h,k) is the center.
.
.
.
The tangent line is perpendicular to the line from (6,7) to (1,4).
Since the second circle is also tangent at the same point, the tangent line is the same line so the center of the new circle must lie on the perpendicular line from (6,7) to (1,4).
The change in x and y from (6,7) to (1,4) must be the same as from (1,4) to (h,k).
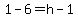

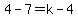

(-4,1)
.
.
.

|
|
|