Question 957815: PQ, PR and QR are tangents to a circle at point S, U and T respectively. Given that PQ=20cm, PR=18cm and QR=16cm, calculate the length of PS, QT and RU(P, Q and R form a triangle)
I tried to use (sin cos tan), but then i realised it wasn't right angled triangle, but the answer shown in my book is
PS=11
QT=9
RU=7
i tried drawing the whole diagram on paper but still cant find the answer. But the weird thing is, the book doesnt show ways to calculate this kind of question. And this is a maths question, but both my maths and add maths teachers doesnt know how to do it(they are good teachers).
I hope that u guys can help me with this question. Ty in advance~
Found 2 solutions by Fombitz, Alan3354:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! If we take the bisector from each corner and find the intersection of the bisectors, that will be the center of the inscribed circle.
The distance from the center of the circle to each side of the triangle will be equal to the incenter circle radius.
If you make the triangle PQR, then it's true that,



I'll call  the center of the inscribed circle. the center of the inscribed circle.
So then 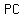 , ,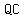 ,and ,and 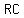 , are the lengths of the bisectors from each vertex. , are the lengths of the bisectors from each vertex.
You can form right triangles
 with legs with legs 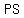 , , 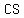 , and hypotenuse , and hypotenuse 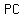 . .
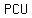 with legs with legs 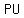 , , 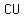 , and hypotenuse , and hypotenuse 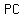 . .
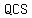 with legs with legs  , , 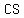 , and hypotenuse , and hypotenuse 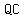 . .
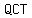 with legs with legs 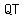 , , 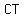 , and hypotenuse , and hypotenuse 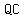 . .
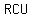 with legs with legs 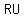 , , 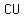 , and hypotenuse , and hypotenuse 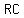 . .
 with legs with legs 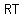 , , 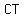 , and hypotenuse , and hypotenuse 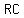 . .
but

So then since the triangles share two equal sides and an angle then,



Then substituting from above,

1.
.
.

2.
.
.

3.
Substracting 1 from 3,

4.
Then adding 2 and 4,



Then,


and finally,


So then,



Answer by Alan3354(69443)   (Show Source): (Show Source):
|
|
|