|
Question 955642: A(2,-1), B(-3,4) and C(1,-5) form the vertices of a triangle. find the interior angles of the triangle
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39621)   (Show Source):
You can put this solution on YOUR website! Would telling you that you should use Distance Formula and then Law Of Cosines be enough for you to analyze and solve the problem?
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
You could do it using the distances and the law of cosines, but
it would be harder that way. I'm sure your teacher wants you
to do it the following way instead, where we find the angle
between two lines:
A(2,-1), B(-3,4) and C(1,-5) form the vertices of a triangle. find the interior angles of the triangle:
We use the slope formula to find the slopes of the sides of the
triangle:
The slope of AB is -1
The slope of BC is -2.25
The slope of AC is 4
The angle q between two lines is given by
∠A is between AB and AC which we can see is obtuse
(greater than 90°.
Substitute the slopes of AB and AC
Now find the reference angle from a calculator using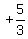 
and inverse tangent feature:
reference angle = 59.03624347°
But we can see that ∠A between the two lines AB and AC
is obtuse, so its tangent is negative and ∠A is a second
quadrant angle so we subtract from 180° and get
∠A = 120.9637565°
------------
Substitute the slopes of AB and BC
∠B is between AB and BC which we can see is acute
(less than 90°.
Substitute the slopes
Now find the reference angle from a calculator using +0.3846153846
and inverse tangent feature:
reference angle = 21.03751103°
We can see that ∠A between the two lines AB and BC
is acute, so the tangent is positive so ∠B is the same
as its reference angle, so
∠B = 21.03751103°
--------------------------------------
To find ∠C, you could do it the same way as the others, but
the easy way is to add ∠A and ∠B and subtract from 180°. So,
∠C = 37.99873244°
Edwin
|
|
|
| |
