|
Question 941934: Let L denote the line passing through the point (6, 9) and the center of the circle (x - 4)2 + (y - 6)2 = 36.
Find the slope of L. Decimal approximations will be marked incorrect.
Answer: 3/2
This is what I'm having trouble with:
Write an equation for L in terms of the variables x and y. Decimal approximations will be marked incorrect.
I'm not sure what it wants? I tried using the point-slope form as y=(3/2)(x-6)+9, but it said that was incorrect.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
the line passing through the point ( , ,  ) and the ) and the 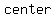 ( ( , , ) of the circle ) of the circle 
since  we know that we know that  and and  (recall the circle formula (recall the circle formula  ) )
so, we have two points the point ( , ,  ) and the point ( ) and the point ( , ,  ) )
now find equation of a line passing through these two points:
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (6, 9) and (x2, y2) = (4, 6).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(1.5)x + (0)
Your graph:

|
since equation is  which is which is  ; so, the slope is ; so, the slope is 
|
|
|
| |