SOLUTION: Help me please circumscribed about the triangle with sides x-y=0 , x+2y=0 and 4x+y=35?

Algebra ->  Circles -> SOLUTION: Help me please circumscribed about the triangle with sides x-y=0 , x+2y=0 and 4x+y=35?      Log On


   

Question 939836: Help me please circumscribed about the triangle with sides x-y=0 , x+2y=0 and 4x+y=35?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I assume you want the equation of the circle whose sides lie on the lines with equations
red%28x-y=0%29 , blue%28x%2B2y=0%29 and green%284x%2By=35%29 .

We need to know the center of the circle and its radius.
If we find where the vertices of the triangle are,
we can figure out where the center of the circle is,
and we can calculate the radius of the circle.

Where are the vertices of the triangle?
They are in points that are on two of those lines at the same time.
system%28x-y=0%2Cx%2B2y=0%29--->system%28x=y%2Cx%2B2y=0%29--->system%28x=0%2Cx%2B2x=0%29--->system%28x=0%2Cy=0%29 gives us pointO%280%2C0%29 .
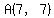system%28x-y=0%2C4x%2By=35=0%29--->system%28x=y%2C4x%2Bx=35=0%29--->system%28x=y%2C5x=35%29--->system%28x=y%2Cx=35%2F5%29--->system%28x=7%2Cy=7%29 gives us pointA%287%2C7%29 .
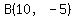system%28x%2B27y=0%2C4x%2By=35=0%29--->system%28x=-2y%2C-8y%2By=35=0%29--->system%28x=-2y%2C-7y=35%29--->system%28x=-y%2Cy=35%2F%28-7%29%29--->system%28x=10%2Cy=-5%29 gives us pointB%2810%2C-5%29 .
So, from now on, I can call it the triangle ABO.

Since the center has to be at the same distance from all 3 vertices of the triangle.
The 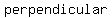perpendicular bisector of a segment is a line containing all the points that are at the same distance from the ends of the segment.
It is perpendicular to the segment.
and goes through the midpoint of the segment.

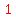Side 0A is part of the line x-y=0<--->y=x , with slope red%281%29 .
The perpendicular bisector of OA contains all the points at the same distance from points O and A.
Its slope is -1%2Fred%281%29=-1 .
It goes through the midpoint, M, of segment OA, whose coordinates are
x%5BM%5D=%28x%5BO%5D%2Bx%5BA%5D%29%2F2=%280%2B7%29%2F7=7%2F2=3.5 , and
y%5BM%5D=%28y%5BO%5D%2By%5BA%5D%29%2F2=%280%2B7%29%2F7=7%2F2=3.5 .
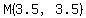The line with slope -1 , going through M%283.5%2C3.5%29 has the equation
y-3.5=-1%28x-3.5%29<-->y-3.5=-x%2B3.5<-->y=-x%2B3.5%2B3.5<-->y=-x%2B7 .

Side 0B is part of the line x%2B2y=0<--->2y=-x<--->y=-x%2F2<--->y=blue%28-1%2F2%29x ,
with slope 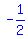blue%28-1%2F2%29 .
The perpendicular bisector of OB contains all the points at the same distance from points O and B.
Its slope is -1%2Fblue%28-1%2F2%29=2 .
It goes through the midpoint, P, of segment OB, whose coordinates are
x%5BP%5D=%28x%5BO%5D%2Bx%5BB%5D%29%2F2=%280%2B10%29%2F2=10%2F2=5 , and
y%5BP%5D=%28y%5BO%5D%2By%5BB%5D%29%2F2=%280%2B%28-5%29%29%2F2=-5%2F2=-2.5 .
The line with slope 2 , going through P%285%2C-2.5%29 has the equation
y-%28-2.5%29=2%28x-5%29<-->y%2B2.5=2x-10<-->y=2x-10-2.5<-->y=2x-12.5 .

Let me add those two lines (the two perpendicular bisector we found) to the drawing:

The point where the two latest lines intersect is at the same distance from points O, A, and B. It is the center of the circle circumscribed about the triangle ABO.
What are the coordinates of that point (the center of the circle we want)?
Since it is on the lines represented by equations
y=-x%2B7 and y=2x-12.5 ,
the coordinates of that point are the solution set to the system
system%28y=-x%2B7%2Cy=2x-12.5%29--->system%28y=-x%2B7%2C-x%2B7=2x-12.5%29--->system%28y=-x%2B7%2C12.5%2B7=2x%2Bx%29--->system%28y=-x%2B7%2C19.5=3x%29--->system%28y=-x%2B7%2Cx=19.5%2F3%29--->system%28y=-6.5%2B7%2Cx=6.5%29--->system%28x=6.5%2Cy=0.5%29 .
What is the radius of that circle?
It is the distance between the center and any point on the circle, such as point O%280%2C0%29 .
That is sqrt%286.5%5E2%2B0.5%5E2%29=sqrt%2842.25%2B0.25%29=sqrt%2842.5%29 .
The equation of the circle is %28x-6.5%29%5E2%2B%28y-0.5%29%5E2=42.5