We have the center of the circle (h,k) = (4,1), and the
equation of a circle:
becomes
So all we are lacking is r, the radius.
We sketch the graph approximately:
The green line is a radius, and it is the perpendicular
distance from the center to the line. We use this formula:
The perpendicular distance from the point (x1,y1)
to the line Ax+By+C=0 is given by this formula:
d = 
(x1,y1) = (4,1)
3x+4y-2=0 is Ax+By+C=0, so A=3, B=4, C=-2
r = 
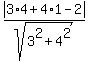r =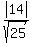 
r = 
r =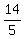 
So the equation of the circle is:
Edwin
