|
Question 916844: find k if the line through (5,11) and (-3,7) is parallel to the line through (-2,k) and (2,5).
Found 2 solutions by MathLover1, DrBeeee:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (5, 11) and (x2, y2) = (-3, 7).
Slope a is  .
Intercept is found from equation  , or  . From that,
intercept b is  , or  .
y=(0.5)x + (8.5)
Your graph:
|
if lines are parallel, they have same slope;
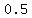 will be a slope of the line through (-2,k) and (2,5)
use (2,5) to find 
now we have: 
use (-2,k) to find 
so,  is parallel to
Answer by DrBeeee(684)  (Show Source):
You can put this solution on YOUR website! Two lines are parallel if their SLOPES are equal.
The slope of a line is (difference in the y coordinates}/(difference in the x coordinates).
The slope of the first line is (11-7)/(5-(-3)) or 4/8 or 1/2
The slope of the second line is (k-5)/(-2-2) or (k-5)(-4).
Now set the slopes equal to each other to get
(k-5)(-4) = 1/2 or
(k-5) =(-4)/2 or
k = 5 - 2 or
k = 3
Let's check this.
Is ((3-5)/(-4) = 1/2)?
Is (-2/(-4) = 1/2)?
Is (1/2 = 1/2)? Yes
Answer: When k = 3 the lines are parallel.
|
|
|
| |
