Question 909337: Diagram of circle with outer edge shaded. The outer circle has diameter 8 inches. The area of the shaded ring is equal to the are of the inner, non-shaded circle. What is the radius of the inner circle? Express your answer as a decimal to the nearest tenth.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Diagram of circle with outer edge shaded. The outer circle has diameter 8 inches. The area of the shaded ring is equal to the are of the inner, non-shaded circle. What is the radius of the inner circle? Express your answer as a decimal to the nearest tenth.
Let radius of smaller, non-shaded, inner circle, be r
Then area of smaller, non-shaded circle is: 
Now, since the area of the smaller, non-shaded circle and the shaded area are equal, then
the area of the smaller, non-shaded circle and the shaded region = 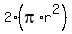 , or , or 
Area of larger circle is: 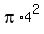 , or , or 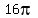
Therefore, we get: 
 ------ Factoring out GCF, ------ Factoring out GCF, 

r, or radius of smaller, non-shaded, inner circle =  , or , or 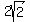 , or , or 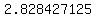 ≈ ≈  inches inches
|
|
|