SOLUTION: Find the sqaure of the length of the tangent to the point (-4,1) on the circle given by the equation x^2+y^2+8x+12y+5=0.

First we put the circle's equation, which is in GENERAL form: 



in STANDARD form





Rearrange the terms so that the x term is just right of the x2 term,
and the y term is just right of the y2 term, and the
constant term is on t he right.



Now we do some work to the side to find the number necessary to 
complete the square on :

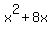1. Multiply the coefficient of x, which is 8, by , getting 4.
2. Square 4, getting 16.
3. Add +16 just after 8x on the left and also add +16 to the right side.



Also to the side we find the number necessary to 
complete the square on :

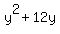1. Multiply the coefficient of y, which is 12, by , getting 6.
2. Square 6, getting 36.
3. Add +36 just after 12y on the left and also add +36 to the right side.


 
Factor the first three terms on the left as  and write as


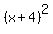Factor the last three terms on the left as  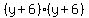and write as
 

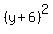Combine the numbers on the right as 35.

Now we have the standard form of the circle:



Comparing to



We see that -h=+4 or h=-4, -k=+6 or k=-6, r2=47,
r=.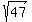

Now we can sketch the graph of the circle with center O(-4,-6) 
and radius 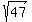. Wow, as we see, the point P(-4,1) is
very close to the circle!. I'll draw the tangent line PT in red,
and the radius to the point of tangency and the line from the 
center to P(4,1) in green.  We want to find the length of PT.
The line OP is 7 units because it's directly above O, which is 6
units below the x-axis, to P which is 1 unit above the x-axis, so
OP is 6+1 or 7 units, and OT is 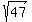. Triangle POT is a
right triangle, so by the Pythagorean theorem:














Edwin