SOLUTION: Find the equation of the bisector of the obtuse angle formed by the lines x + 2y - 3 = 0 and 2x + y - 4 = 0. Thanks.

Algebra ->  Points-lines-and-rays -> SOLUTION: Find the equation of the bisector of the obtuse angle formed by the lines x + 2y - 3 = 0 and 2x + y - 4 = 0. Thanks.      Log On


   

Question 903672: Find the equation of the bisector of the obtuse angle formed by the lines x + 2y - 3 = 0 and 2x + y - 4 = 0.
Thanks.
Found 2 solutions by Edwin McCravy, Theo:
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
 x + 2y - 3 = 0 
2x +  y - 4 = 0

These are the black lines in the graph below:



Let the variable point (x,y) be any point on the bisector of the
obtuse angle between the two black lines.

Then the perpendicular distances from (x,y) to each of 
those lines (the lengths of the two green line segments) are equal. 

The formula for the perpendicular distance from the point (x1,y1)
to the line Ax+y+C=0 is:

d = abs%28Ax%5B1%5D%2BBy%5B1%5D%2BC%29%2Fsqrt%28A%5E2%2BB%5E2%29

So we substitute (x1,y1) = (x,y) 
for the first line:

x + 2y - 3 = 0,  A=1, B=2, C=-3

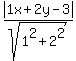d = abs%281x%2B2y-3%29%2Fsqrt%281%5E2%2B2%5E2%29
 
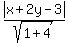d = abs%28x%2B2y-3%29%2Fsqrt%281%2B4%29

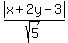d = abs%28x%2B2y-3%29%2Fsqrt%285%29

And also for the second line:

2x +  y - 4 = 0,  A=2, B=1, C=-4

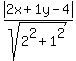d = abs%282x%2B1y-4%29%2Fsqrt%282%5E2%2B1%5E2%29

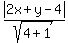d = abs%282x%2By-4%29%2Fsqrt%284%2B1%29

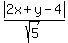d = abs%282x%2By-4%29%2Fsqrt%285%29

We set those distances equal:

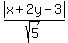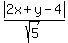abs%28x%2B2y-3%29%2Fsqrt%285%29%22%22=%22%22abs%282x%2By-4%29%2Fsqrt%285%29

Multiply both sides by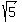 sqrt%285%29

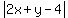abs%28x%2B2y-3%29%22%22=%22%22abs%282x%2By-4%29

This breaks into two equations.  One is the angle bisector of the
acute angle and the other is the equation of the bisector of the
obtuse angle (the one we want).

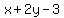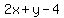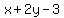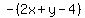
x%2B2y-3%22%22=%22%222x%2By-4  and  x%2B2y-3%22%22=%22%22-%282x%2By-4%29
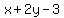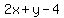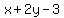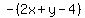
x%2B2y-3%22%22=%22%222x%2By-4  and  x%2B2y-3%22%22=%22%22-%282x%2By-4%29
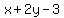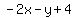-x%2By%2B1=0                      and  x%2B2y-3%22%22=%22%22-2x-y%2B4 
                                     and  3x%2B3y-7=0

We can see by the graph that the dotted line has a positive slope, and
that the line bisecting the acute angle between the two black lines has
a negative slope.

We put the two lines in slope intercept form

-x%2By%2B1=0    3x%2B3y-7=0
   y=x-1       3y=-3x%2B7
                     y=-x%2B7%2F3

And we see that the first one has a positive slope, so the answer
is 

y=x-1

The other line y=-x%2B7%2F3 is the purple dotted line below.
It has a negative slope, which as you can see, bisects the acute 
angle between the two black lines:



But the answer that we want is the red dotted line, which 
has equation:

y=x-1

Edwin

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
I don't know if there's an easy way to do this, but I did find what looks like an answer that makes sense, even though it took a rather large effort to find it.

you can find the slope of both lines by converting them to the slope intercept form of their equations.

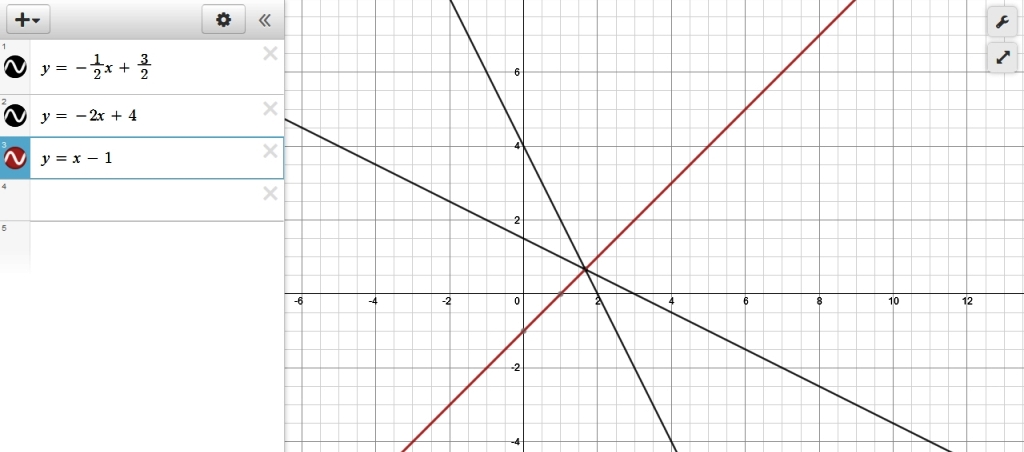
x + 2y - 3 = 0 becomes y = -1/2x + 3/2

2x + y - 4 = 0 becomes y = -2x + 4

the slope of the first line is -1/2
the slope of the second line is -2

you can find each of the angles formed by these lines by finding their arctangents.

the angle formed by the first line is equal to arctan(-1/2) = -26.56505118 degrees.

the angle formed by the second line is equal to arctan(-2) = -63.43494882 degrees.

those would be the angles in quadrant 4.

those 2 lines intersect at the point (5/3, 2/3).

that intersection can be found by solving both equations simultaneously.

I chose the easy way and solved by graphing.

you could also solve by substitution or by elimination.

you'll get the same answer either way.

at that intersection point, you are looking at 2 lines that have a rather large obtuase angle between them.

to find the bisector of that angle, you first have to find that angle.

at least I think you do and that's the method I chose.

Those angles are found by looking at them in reference to the horizontal line that goes through their intersection point.

one of the angles is -26.56505118 degrees.
the other angle is is the quadrant 2 equivalent of -63.43494882 degrees.

the quadrant 2 equivalent of -63.43494882 degrees is equal to 116.5650512 degrees.

The large obtuse angle is therefore 116... + 63... which is equal to 143.1301024 degrees.

half of that is equal to 71.5650512 degrees.

the angle that you want to find the slope of is going to be 116.5650512 - 71.5650512 degrees which is equal to 45 degrees.

this angle is the same as the angle found by adding 71.5650512 to -26.5650512 degrees which is also equal to 45 degrees.

so the angle bisector of the obtuse angle appears to be 45 degrees which has a tangent of 1.

the slope of the line is therefore equal to 1.

the line will intersect at the point (5/3, 2/3).

solve for b in the equation of y = 1x + b when x = 5/3 and y = 2/3 and you get:

2/3 = 1 * (5/3) + b which becomes 2/3 = 5/3 + b which becomes b = -3/3 which becomes b = -1.

the equation of the line that bisects the obtuse angle is therefore equal to:

y = x - 1

the following graph shows all 3 lines and it should be fairly easy to see that the line y = x - 1 appears to bisect the obtuse angle formed by the intersection of the other 2 lines.

$$$

I'm reasonably confident the answer is correct even if I had to go through hoops to find it.

I tried to think of an easier way to do it but drew a blank.