SOLUTION: There are two concentric circles, whose areas are in the ratio 0.25. Determine the center if a straight line drawn from the center intersects the smaller and bigger circles at (2,

Algebra ->  Circles -> SOLUTION: There are two concentric circles, whose areas are in the ratio 0.25. Determine the center if a straight line drawn from the center intersects the smaller and bigger circles at (2,       Log On


   

Question 897347: There are two concentric circles, whose areas are in the ratio 0.25. Determine the center if a straight line drawn from the center intersects the smaller and bigger circles at (2, 3) and (4, 8) respectively.
My answer is (0, -2). Am I correct? Please show me the working.
Answer by reviewermath(1029) About Me  (Show Source):
You can put this solution on YOUR website!
Q:
There are two concentric circles, whose areas are in the ratio 0.25. Determine the center if a straight line drawn from the center intersects the smaller and bigger circles at (2, 3) and (4, 8) respectively.
My answer is (0, -2). Am I correct? Please show me the working.
A:
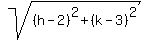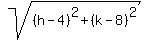If (h,k) is the center of the circle, then the radius of the smaller circle is equal to sqrt%28%28h-2%29%5E2%2B%28k-3%29%5E2%29 and the radius of the bigger circle is sqrt%28%28h-4%29%5E2%2B%28k-8%29%5E2%29. The ratio of the area of the smaller circle to the area of the bigger circle is equal to
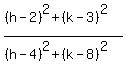%28%28h-2%29%5E2%2B%28k-3%29%5E2%29%2F%28%28h-4%29%5E2%2B%28k-8%29%5E2%29 = 0.25
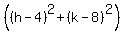
%28%28h-2%29%5E2%2B%28k-3%29%5E2%29 = 0.25%28%28h-4%29%5E2%2B%28k-8%29%5E2%29
Multiply both sides by 4 and expand.
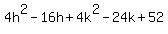4h%5E2-16h%2B4k%5E2-24k%2B52 = h%5E2-8h%2Bk%5E2-16k%2B80
3h%5E2-8h%2B3k%5E2-8k-28+=+0
The equation of the straight line is y = 2.5x - 2 so k = 2.5h - 2
3h%5E2-8h%2B3%282.5h+-+2%29%5E2-8%282.5h+-+2%29-28+=+0
3h%5E2-8h%2B3%286.25h%5E2-10h%2B4%29-20h-12+=+0
3h%5E2-8h%2B18.75h%5E2-30h%2B12-20h-12+=+0
21.75h%5E2-58h+=+0
Multiply both sides by 4.
87h%5E2-232h+=+0
Divide both sides by 29
3h%5E2-8h+=+0
h(3h - 8) = 0
h = 0 or h = 8/3
Using the equation k = 2.5h - 2.
If h = 0, then k = -2.
If h = 8/3, then k = 14/3.
There are two possible answers.
They are (0, -2) or (8/3, 14/3).