SOLUTION: Dear Sir/Madam; Please help me with this problem: An arch is built in the form of an arc of a circle and is subtended by chord 30 ft. long. If a chord 17 ft. long subtends h

These pictures represent the same arch.  Arc CD is half as long as arc AB.

Since arcs are measured by their central angles, we will draw in radii to
the endpoints of the arcs and also draw perpendiculars from the center O
to the chords.  The perpendiculars will divide the chords in half as well
as the central angles.  We will let the radius be r.



Since arc CD is half as long as arc AB, arc AB is twice
as long as arc CD. Therefore the central angle AOB that 
subtends arc AB is twice the measure of the central angle
that subtends arc CD.

Therefore half the angle AOB, which is EOB is twice half
the angle COD, which is FOD.  Therefore we mark angle FOD
as  and angle EOB as 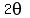.  Then

Using right triangle EOB:





Using right triangle FOD,





Setting the two expressions for r equal:




Using the identity for the sine of twice an angle:



Using the zero-factor property, set each equal to 0:

, 

The first equation has solutions 0°,180°,360°
That would be the case when arc AB was the entire 
circle and and arc CD was a half circle or semicircle.
That is a feasible answer mathematically, but it is not
what we want because we are told we only have an arch,
not an entire circle.  So we disregard this answer.





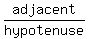Since the cosine is , we draw a 
right triangle containing  with adjacent side = 15 
and hypotenuse = 17.





Since:



Edwin