Question 893194: Find the equation of the circle inscribed in a triangle, if the triangle has its sides on the lines 2x+y-9=0, -2x+y-1=0, -x+2y+7=0. Draw the figure
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation of the circle inscribed in a triangle, if the triangle has its sides on the lines 2x+y-9=0, -2x+y-1=0, -x+2y+7=0. Draw the figure
-----------
Idk any shortcuts, just have to grind it out.
Find the intersections, then the lengths of the sides:
---
2x +y-9=0
-2x+y-1=0
------------- Add
2y -10 = 0
y = 5
x = 2
Point A(2,5)
----
-2x+y-1=0
-x+2y+7=0
Point B(-3,-5)
----
2x+y-9=0
-x+2y+7=0
Point C(5,-1)
----------------
Find the lengths AB, BC and AC
side c = 
c = 
b = 
a = 
It's a right triangle, btw. Sides of 3, 4 & 5 times sqrt(5)
----
The center of the circle is on the intersection of the bisectors of the 3 angles.
The intersection of any 2 bisectors is the center.
Find the slope of the 3 sides:
2x+y-9=0, -2x+y-1=0, -x+2y+7=0
Put each of the 3 original eqns in slope-intercept form.
2x+y-9=0
y = -2x + 9
m = -2 (slope of AC)
----
-2x+y-1=0
y = 2x + 1
m = 2 (slope of BA)
----
-x+2y+7=0
y = x/2 - 7/2
m = 1/2 (slope of BC)
========================
The slopes are AC and BA are opposites, so the bisector of A is vertical (parallel to the y-axis).
--> the center of the circle is on the line x = 2.
==============
Using r = a*b/(a+b+c), the radius of the circle = sqrt(5)
---
The intersection of the bisector of A and side BC is (2,-2.5) (point D)
Distance DC = 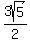
---------
Triangles ACD and AEO are similar, so
AD/DC = AO/OE
AD = 15/2
7.5/(3sqrt(5)/2) = AO/sqrt(5)
AO = 5
===========
--> The center is (2,0)
---------
The circle is 
======================
I'll send a graph if you respond via the TY note.
|
|
|