SOLUTION: PLEASE HELP ME. FIND THE EQUATION OF A CIRCLE PASSING THROUGH (3,7) AND TANGENT TO THE LINES {{{ x - 3y + 8 = 0 }}} AND {{{ y = 3x }}}.

Algebra ->  Circles -> SOLUTION: PLEASE HELP ME. FIND THE EQUATION OF A CIRCLE PASSING THROUGH (3,7) AND TANGENT TO THE LINES {{{ x - 3y + 8 = 0 }}} AND {{{ y = 3x }}}.      Log On


   

Question 876850: PLEASE HELP ME. FIND THE EQUATION OF A CIRCLE PASSING THROUGH (3,7) AND TANGENT TO THE LINES +x+-+3y+%2B+8+=+0+ AND +y+=+3x+.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
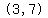PLEASE HELP ME. FIND THE EQUATION OF A CIRCLE PASSING THROUGH +%22%283%2C7%29%22+ AND TANGENT TO THE LINES +x+-+3y+%2B+8+=+0+ AND +y+=+3x+.
Draw the two lines and the point (3,7)



Those two lines intersect at (1,3).

Visually, it appears that there are two solutions:



Let's just look at one of them to keep things simple.

Suppose the center of the circle is (h,k)


The two green and the one red lines are radii of the desired
circle. The two green radii represent the perpendicular (shortest)
distances from (h,k) to each of the two lines.

The formula for the perpendicular distance from the point 

(x1,y1)

to the line Ax+y+C=0 is

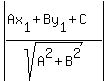d = abs%28%28Ax%5B1%5D%2BBy%5B1%5D%2BC%29%2Fsqrt%28A%5E2%2BB%5E2%29%29

The lines are 1x-3y+8=0 and 3x-1y+0=0
So for the first line A=1, B=-3, C=8
For the second line A=3, B=-1, C=0

(x1,y1) = (h,k)

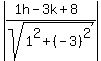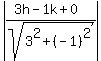
abs%28%281h-3k%2B8%29%2Fsqrt%281%5E2%2B%28-3%29%5E2%29%29 = abs%28%283h-1k%2B0%29%2Fsqrt%283%5E2%2B%28-1%29%5E2%29%29

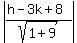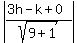
abs%28%28h-3k%2B8%29%2Fsqrt%281%2B9%29%29 = abs%28%283h-k%2B0%29%2Fsqrt%289%2B1%29%29

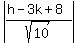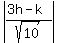abs%28%28h-3k%2B8%29%2Fsqrt%2810%29%29 = abs%28%283h-k%29%2Fsqrt%2810%29%29

Multiplying through by sqrt%2810%29

|h-3k+8| = |3h-k|

There are two possibilities for that:

h-3k+8 = 3h-k    and   h-3k+8 = -(3h-k)
   -2k = 2h-8          h-3k+8 = -3h+k 
     k = -h+4             -4k = -4h-8 
     k = 4-h                k = h+2

Looking at the graph we can tell that  
the first one cannot be correct. because 
k=4-h would be saying that the sum of 
coordinates of (h,k), k+h = 4. The point
(h,k) is even further to the right and
higher than (1,3) where the two lines
intersect. (1,3) has sum of coordinates 
4, so the sum of coordinates h and k has
to be more than 4.  Therefore 

k = h+2.

Now we equate the red radius to one of the
green radii. We use the distance formula between
two points for the red radius:

d = √(x2-x1)²+(y2-y1)²  

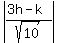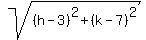 abs%28%283h-k%29%2Fsqrt%2810%29%29 = sqrt%28%28h-3%29%5E2%2B%28k-7%29%5E2%29

Squaring both sides we have:

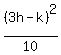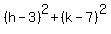%283h-k%29%5E2%2F10 = %28h-3%29%5E2%2B%28k-7%29%5E2%29

Multiplying both sides by 10

(3h-k)² = 10[(h-3)² + (k-7)²]

Substituting k = h+2 from above:

[3h-(h+2)]² = 10[(h-3)² + ((h+2)-7)²]

[3h-h-2]² = 10[(h-3)² + (h+2-7)²]

(2h-2)² = 10[(h-3)² + (h-5)²]

4h²-8h+4 = 10[h²-6h+9 + h²-10h+25]

4h²-8h+4 = 10(2h²-16h+34)

Divide both sides by 2

2h²-4h+2 = 5(2h²-16h+34)

2h²-4h+2 = 10h²-80h+170

-8h²+76h-168 = 0

Divide through by -4

2h²-19h+42 = 0

(2h-7)(h-6) = 0

2h-7 = 0;   h-6 = 0
  2h = 7;     h = 6
   h = 7%2F2;   

When h=7%2F2, k = h+2 = 7%2F2+2 = 7%2F2%2B4%2F2 = 11%2F2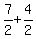

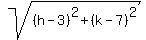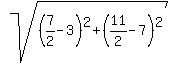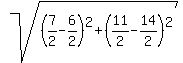And the red radius = sqrt%28%28h-3%29%5E2%2B%28k-7%29%5E2%29 = sqrt%28%287%2F2-3%29%5E2%2B%2811%2F2-7%29%5E2%29 = sqrt%28%287%2F2-6%2F2%29%5E2%2B%2811%2F2-14%2F2%29%5E2%29 = 
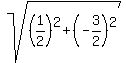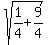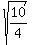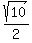sqrt%28%281%2F2%29%5E2%2B%28-3%2F2%29%5E2%29 = sqrt%281%2F4%2B9%2F4%29 = sqrt%2810%2F4%29 = sqrt%2810%29%2F2

So the equation of one circle is

(x-h)²+(y-k)² = r²

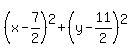
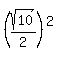
%28x-7%2F2%29%5E2%2B%28y-11%2F2%29%5E2%22%22=%22%22%28sqrt%2810%29%2F2%29%5E2

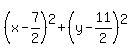
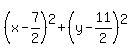
%28x-7%2F2%29%5E2%2B%28y-11%2F2%29%5E2%22%22=%22%2210%2F4

%28x-7%2F2%29%5E2%2B%28y-11%2F2%29%5E2%22%22=%22%225%2F2

That's one solution.

When h=6, k = h+2 = 6+2 = 8

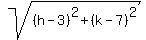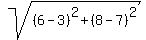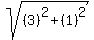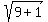And the red radius = sqrt%28%28h-3%29%5E2%2B%28k-7%29%5E2%29 = sqrt%28%286-3%29%5E2%2B%288-7%29%5E2%29 = sqrt%28%283%29%5E2%2B%281%29%5E2%29 = sqrt%289%2B1%29 = sqrt%2810%29

So the equation of the other circle is

(x-h)²+(y-k)² = r²

%28x-6%29%5E2%2B%28y-8%29%5E2%22%22=%22%2210

That's the other solution.

Edwin