|
Question 826947: If the line passing through the points
(a, 1) and (−10, 9)
is parallel to the line passing through the points
(−3, 8) and (a + 2, 1),
what is the value of a?
Answer by LinnW(1048)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two parallel lines
one through (a,1) and (-10,9) and another through (-3,8) and (a+2,1)
Since parallel lines have the same slope we can
use the general equation for slope
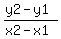
For (a,1) and (-10,9) , x1=a x2=-10 y1=1 y2=9
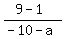 = = 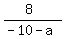
For (-3,8) and (a+2,1) , x1=-3 x2=a+2 y1=8 y2=1
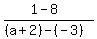 = = 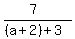 = =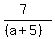
Now set the two slope equations to be equal
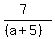 = =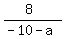
do cross products

-70 -7a = 8a + 40
add 70 to each side
-7a = 8a + 110
add -8a to each side
-15a = 110
divide each side by -15
a = -110/15
a = -22/3
Checking
For (a,1) and (-10,9) , x1=a x2=-10 y1=1 y2=9
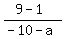 ?= ?= 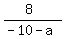
with a = -22/3
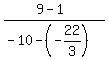 ?= ?= 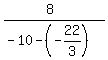
?= 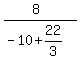

 = -3 = -3
So we have the slope for the first set of points = -3
Let's look at the second set.
For (-3,8) and (a+2,1) , x1=-3 x2=a+2 y1=8 y2=1
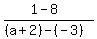 = = 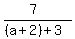 = =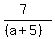
with a = -22/3

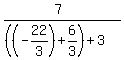
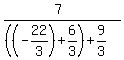
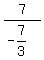 = -3 = -3
So we see that a = -22/3 produces two lines with the same -3 slope.
|
|
|
| |