SOLUTION: P(4,2) point on circle x^2+y^2=5x If PQ is a diameter of the circle find the coordinates of Q

Algebra ->  Circles -> SOLUTION: P(4,2) point on circle x^2+y^2=5x If PQ is a diameter of the circle find the coordinates of Q      Log On


   

Question 826622: P(4,2) point on circle x^2+y^2=5x
If PQ is a diameter of the circle find the coordinates of Q
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Use the point and see what happens:

%284%29%5E2%2B%282%29%5E2=5%2A4
16%2B4=20
20=20
Good so far.

We MUST have radius*radius=20.
The circle is centered at the origin. The form of the equations tells that.
Radius is 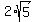2%2Asqrt%285%29.
The equation for the circle is x%5E2%2By%5E2=20

What have we now?
The center of the circle is (0,0), based on the equation for it; and the radius is sqrt%2820%29. Point P(4,2) is a point on the circle and we WANT the endpoint of the diameter other than P.

We also expect the diameter to contain both P and the origin (0,0). What is the line for these two points? The both endpoints of the diameter must be on this line!

Line defined by (0,0) and (4,2):
slope is (1/2). Obviously runs through origin.
Equation for line is y=%281%2F2%29x.

What points are on this line AND are sqrt(20) distance from the origin (0,0)? We look for points (x,y), as (x,(1/2)x).
USE DISTANCE FORMULA.
'
sqrt%2820%29=sqrt%28%28x-0%29%5E2%2B%28%281%2F2%29x-0%29%5E2%29
20=x%5E2%2B%281%2F4%29x%5E2
%28x%5E2%29%281%2B1%2F4%29=20
%285%2F4%29x%5E2=20
x%5E2=%284%2F5%2920=16
x=0%2B-+4

We already know about x=4 based on our given point on the circle. We use the equation for the line y=%281%2F2%29x to find the OTHER endpoint for the diameter. Use x=-4 to find the y value for this endpoint:
y=%281%2F2%29%28-4%29
y=-2
FINISHED ANSWER: The other endpoint for the diameter at opposite end from (4,2) is (-4,-2).
DONE!

-Most of solution above was modified and corrected-