SOLUTION: The angle from the line through (-1,y) and (4,-7) to the line through (4,2) and (-1,-9) is 135 degrees. Find y

Algebra ->  Points-lines-and-rays -> SOLUTION: The angle from the line through (-1,y) and (4,-7) to the line through (4,2) and (-1,-9) is 135 degrees. Find y      Log On


   

Question 825054: The angle from the line through (-1,y) and (4,-7) to the line through (4,2) and (-1,-9) is 135 degrees. Find y
Answer by Edwin McCravy(20065) About Me  (Show Source):
You can put this solution on YOUR website!


We will use the formula for the angle q between two lines,

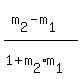tan(q) = %28m%5B2%5D-m%5B1%5D%29%2F%281%2Bm%5B2%5Dm%5B1%5D%29, where q = 135° and tan(135°) = -1

First we must find the two slopes

Let m2 = the slope of the green line, and m1 = the slope of the red line

To find the slopes we use the slope formula:

m2 = %28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
where (x1,y1) = (-1,y)
and (x2,y2) = (4,-7)

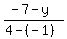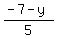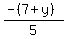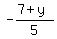m2 = %28-7-y%29%2F%284-%28-1%29%29 = %28-7-y%29%2F%284%2B1%29 = %28-7-y%29%2F5 = %28-%287%2By%29%29%2F5 = -%287%2By%29%2F5

and

m1 = %28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29
where (x1,y1) = (4,2)
and (x2,y2) = (-1,-9)

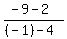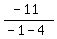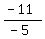m1 = %28-9-2%29%2F%28%28-1%29-4%29 = %28-11%29%2F%28-1-4%29 = %28-11%29%2F%28-5%29 = 11%2F5

And we substitute in the formula for the angle between two
lines:

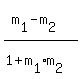tan(q) = %28m%5B1%5D-m%5B2%5D%29%2F%281%2Bm%5B1%5Dm%5B2%5D%29

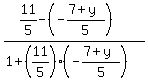tan(135°) = %2811%2F5-%28-%287%2By%29%2F5%29%29%2F%281%2B%2811%2F5%29%28-%287%2By%29%2F5%29%29

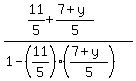-1 = %2811%2F5%2B%287%2By%29%2F5%29%2F%281-%2811%2F5%29%28%287%2By%29%2F5%29+%29%29

Multiply both sides by the denominator on the right:

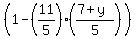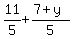
-1%281-%2811%2F5%29%28%287%2By%29%2F5%29+%29%29 = 11%2F5%2B%287%2By%29%2F5%29

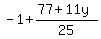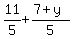-1%2B%2877%2B11y%29%2F25 = 11%2F5%2B%287%2By%29%2F5%29

Multiply through by 25

-25+(77+11y) = 55+5(7+y)
  -25+77+11y = 55+35+5y
      52+11y = 90+5y
          6y = 38
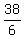           y = 38%2F6
           y = 19%2F3

Edwin