|
Question 819373: find the trisection points of the line joining (-6,2) and (3,8).
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find equation for the line:




Pick either point: (3,8),


Equation is 
Distance between the two points:
Using Distance Formula,

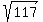
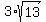
You want a point (x,y) which is distance sqrt(13) away from (-6,2), and another point which is 2*sqrt(13) from (-6,2). Use distance formula.
Your unknown points begin as (x, (2/3)x+6 ), and you must take results for which 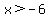 and and 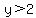 . .
'
continuing this way,

Solve for x and find the corresponding y....
|
|
|
| |