SOLUTION: Find the equation of circle which passes through (1,-2) and (4,-3) and has its centre on line 3x+4y-7=0. N.B. (Please solve with suitable diagram)

Algebra ->  Circles -> SOLUTION: Find the equation of circle which passes through (1,-2) and (4,-3) and has its centre on line 3x+4y-7=0. N.B. (Please solve with suitable diagram)      Log On


   

Question 810707: Find the equation of circle which passes through (1,-2) and (4,-3) and has its centre on line 3x+4y-7=0.
N.B. (Please solve with suitable diagram)
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
The center of the circle is the same distance from (1,-2) as it is from (4,-3). You can solve the equation of the line containing the center of the circle for y so it is in slope-intercept form.

4y=0-3x%2B7
y=-%283%2F4%29x%2B7%2F4.
You have then a general point for the center of the circle, (x, y) or more precisely, (x, -(3/4)x+7/4).

Use Distance Formula for both of the given points on the circle, and the fact that each of them is equally distant from the center of the circle.




%281-x%29%5E2%2B%281%2F16%29%283x-15%29%5E2=%284-x%29%5E2%2B%281%2F16%29%283x-19%29%5E2
16%281-x%29%5E2%2B%283x-15%29%5E2=16%284-x%29%5E2%2B%283x-19%29%5E2
.
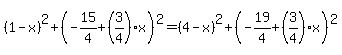
keep going, solving for x...
. ...doing the steps on paper to find x,...
.
.
highlight%28x=47%2F15%29
That is only part of the answer; you can use this x value to find the corresponding y value for the center. Remember the given line containing the center! Again use distance formula to find radius, from either given point to the center of the circle. You would then be able to fill in all parts of the equation for the circle.