SOLUTION: Are the lines parallel, perpendicular, or neither? 3x+4y=12 and 6x+2y=7

Algebra ->  Points-lines-and-rays -> SOLUTION: Are the lines parallel, perpendicular, or neither? 3x+4y=12 and 6x+2y=7      Log On


   

Question 805405: Are the lines parallel, perpendicular, or neither? 3x+4y=12 and 6x+2y=7
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Neither.
If two lines are parallel, they have the same slope.
If two lines are perpendicular, the product of their slopes is -1.

To find the slope we could solve for y to get the slope intercept form of the equation.
We do not really need the intercept. We only need the slope, but it's not hard.
3x%2B4y=12-->4y=-3x%2B12-->y=%28-3%2F4%29x%2B12%2F4-->y=%28-3%2F4%29x%2B3
6x%2B2y=7-->2y=-6x%2B7-->y=%28-6%2F2%29x%2B7%2F2-->y=-3x%2B7%2F2
The slopes are -3%2F4 and -3.
They are not the same number, so the lines are not parallel.
When you multiply them,
%28-3%2F4%29%28-3%29=9%2F4,
you do not get -1, so the lines are not perpendicular either.

Maybe, to find slopes, you've been told that for a linear equation in the form Ax%2BBy=C
(like 3x%2B4y=12 and 6x%2B2y=7),
the slope is 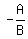-A%2FB,
which means take the coefficient of the x, change its sign, and divide it by the coefficient of the y.
Maybe you are expected memorize formulas and do that.
With3x%2B4y=12, you take the A=3, change it into -A=-3, and divide by B=4 to get -3%2F4
With 6x%2B2y=7), you take the 6, change it to -6, and divide by 2 to get -3