Question 800179: Two circles of equal radii touch each other at point D(p,p).Centre A of the one circle lies on the Y-axis.Point B(8,7) is the centre of the other circle.FDE is a common tangent to both circles..How to calculate the co-ordinates of D when only given a centre with no radius?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Looking at them from some point of view, the circles must look like this:
Point D is at the same distance from the center of both circles, and on the line that connects those centers.
It is the midpoint of segment AB.
Its x-coordinate is the average of the x-coordinates of A and B
The x-coordinate of B(8,7) is 
We know that the x-coordinate of A is zero, because  for all points on the y-axis and A is on the y-axis. So 
So, the x-coordinate of D(p,p) is  ,
meaning that  .
Since it is written as D(p,p), with the same  as x and y-coordinate, it must be D(4,4).
For A(0,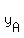 ), that would mean that  ,
and from  we get
 -->  -->  --> 
Also, the radius of the circles is the distance from B(8,7) to D(4,4).
That is
Now, I could draw those circles, with the x- and y-axes, the line connecting their centers, and the common tangent to both circles.
The slope of AB is
The tangent to both circles is perpendicular to AB, so its slope is
 .
The tangent passes through D(4,4) so its equation is
 -->  -->  -->  --> 
We could also write it differently:
 -->  --> 
|
|
|
