Question 792578: I have a circle, diameter 30.85 meters, there is a straight line radiating from the edge (tangent) if you travel 1 meter along this line and turn 90 degrees so you are facing the circle how far away is the edge of the circle? Is there an equation to calculate the distance from this line at regular intervals and to determine at what distance the circle would, in effect, start to return on itself?
Many thanks for your help
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! On an x-y coordinate plane, a circle of radius R has the equation (
Let's say you start at point A(0,R).
If you leave the circle on the tangent at point A(0,R) and travel a distance b you get to point B(b,R).
The radius of the circle going through A is the y-axis, the line  , ,
and the tangent at A is the perpendicular line  . .
If you turn 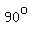 towards the circle, you will travel along the line towards the circle, you will travel along the line  and will get to the circle at point C. and will get to the circle at point C.

Point C has 
We can find the y-coordinate from the equation of the circle.
 --> -->  --> --> 
The distance between points B and C is the difference between their y-coordinates,
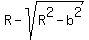
Of course you need to make  . .
Otherwise, when you turn 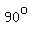 at point B(b,R) you are too far to the right and pass by the circle without ever finding a point C. at point B(b,R) you are too far to the right and pass by the circle without ever finding a point C.
In your case,  is very large compared to is very large compared to  . .
The triangle ABC for that case looks so ridiculously thin that I did not help explain the problem.
The formula above calculates the distance between points B and C as
 = approximately = approximately 
When R is so much larger than b, you can calculate a good approximation with the formula
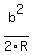 , which in this case would give you , which in this case would give you  = approximately = approximately 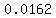
|
|
|