Question 785341: Find the standard form for the equation of a circle with equation (x-h)^2+ (y-k)^2=r2
with a diameter that has endpoints (-5,8) and (9,4)
i got 53 for the radio and found the midpoint coordinates (2,6) however my answer is still wrong, please help me!
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation of a circle with equation 
with a diameter that has endpoints ( , , ) and ( ) and ( , , ) )
first find diameter  which is equal to distance between two given points: which is equal to distance between two given points:
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (-5, 8), we can say (x1, y1) = (-5, 8)
So  , , 
Since the second point is (9, 4), we can also say (x2, y2) = (9, 4)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (-5, 8) and (9, 4)

 Plug in Plug in  , ,  , ,  , and , and 







==========================================================
Answer:
The distance between the two points (-5, 8) and (9, 4) is exactly 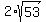 units units
The approximate distance between the two points is about 14.560219778561 units
So again,
Exact Distance: 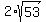 units units
Approximate Distance: 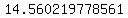 units units
|
since 
now we know that radius is 
now, find coordinates of the center which will be midpoint of diameter:
| Solved by pluggable solver: Midpoint |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (-5, 8), we can say (x1, y1) = (-5, 8)
So  , , 
Since the second point is (9, 4), we can also say (x2, y2) = (9, 4)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
----------------------------------------------------------------------------------------
Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 
So the x coordinate of the midpoint is 2
----------------------------------------------------------------------------------------
Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2
Y Coordinate of Midpoint = 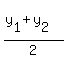
Y Coordinate of Midpoint = 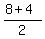
Y Coordinate of Midpoint = 
Y Coordinate of Midpoint = 
So the y coordinate of the midpoint is 6
===============================================================================
Summary:
The midpoint of the segment joining the two points (-5, 8) and (9, 4) is (2, 6).
So the answer is (2, 6)
|
as you can see, the midpoint of the segment joining the two points ( , , ) and ( ) and ( , , ) is ( ) is ( , ,  ) which means ) which means  and and 
so, equation of a circle will be:



|
|
|