Question 783735: Find an equation of a circle tangent to 3x+4y-16=0 at (4,1) with a radius of 5.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an equation of a circle tangent to 3x+4y-16=0 at (4,1) with a radius of 5.
----------------
The line thru the center of the circle is perpendicular to the given line, and the center is 5 units from the tangent points.
---
Find the slope of the line
3x+ 4y = 16
solve for y
y = -3x/4 + 4
Slope of the line = -3/4
Slope of the perpendicular line = 4/3
---
Find the eqn of the perpendicular line thru (4,1)
use y = mx + b and the point to find b, the y-intercept
1 = (4/3)*4 + b
b = -13/3
-----
The perpendicular line is y = 4x/3 - 13/3
---
There are 2 points 5 units from (4,1) on y = 4x/3 - 13/3 --> 2 tangent circles
-----
Draw a circle radius = 5 centered at (4,1)

y = 4x/3 - 13/3
Sub for y
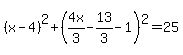
Solve for x



| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=22500 is greater than zero. That means that there are two solutions:  . .
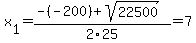

Quadratic expression 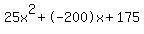 can be factored: can be factored:

Again, the answer is: 7, 1.
Here's your graph:
 |
==============
x = 7, y = 5 --> (7,5)
-->  is one circle is one circle
========================================
x = 1, y = -3 --> (1,-3)
 is the 2nd circle is the 2nd circle
|
|
|