Question 758531: Find the coordinates of a point on a circle at the opposite end of the diameter from point A (-7,-1)? The circle's formula is (x+4)^2+(y-3)^2=25
Found 3 solutions by Alan3354, Edwin McCravy, MathLover1:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find the coordinates of a point on a circle at the opposite end of the diameter from point A (-7,-1)? The circle's formula is (x+4)^2+(y-3)^2=25
------------
The circle's center is (-4,3)
---
--> (-1,7)
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
(x-h)² + (y-k)² = r² has center (h,k) and radius r
compare your equation
(x+4)² + (y-3)² = 25
to that and you see that
-h=+4, so h=-4
-k=-3, so k=3
r²=25, so r=5
Draw a horizontal line from (-7,-1) to a point directly below
the center, then a vertical line from there to the center (4,3).
The horizontal line is 3 units long and the vertical line is
4 units long. Then do the same from the center of the circle,
3 units right from (4,3), then 4 units up, and you end up at
the point (-1,7)
  
Edwin
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website! Find the coordinates of a point on a circle at the opposite end of the diameter from
point A ( , )?
The circle's formula is 
from the circle's formula we can see that radius  ; so, diameter is  , the center is at ( , )
now we can find equation of the line passing through points A (,) and (,):
| Solved by pluggable solver: Find the equation of line going through points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (-7, -1) and (x2, y2) = (-4, 3).
Slope a is  .
Intercept is found from equation  , or  . From that,
intercept b is  , or  .
y=(1.33333333333333)x + (8.33333333333333)
Your graph:
|
if you go three units to the right and four units up from the point (,), you will get to the point (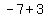 , 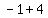)=(,) and distance will be  which is radius
then go three units to the right and four units up from the center (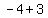 , )=(, ) and distance will be 
or,
If you know the center of the circle, then it is the midpoint of the diameter. You can use the midpoint formula to solve for the  and  values of the other endpoint of the diameter.
-------------------------
---------------------
 =>  => 
 => =>
so, the point is (,)
|
|
|
