Question 692844: A pleasant day Sir/ Madam, my daughter has this problem in geometry and I am not good in geometric proofs, can you please help me?
the illustration or drawing is a rectangle inscribed in a circle
Given: Quadrilateral ABCD is a rectangle
Prove: line segment AC and line segment BD are diameters of the circle
Thank you very much for anyone who can help me!
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
first draw the picture:

next, we will need to prove this:
theorem: Diagonal of any rectangle inscribed in a circle is a diameter of the circle. (
This is essentially the converse of Thales' theorem.
Let A, B, C and D be the vertices of a rectangle inscribed in a circle and let AC and BD be the diagonals of this rectangle.
We can now focus on any one of the four triangles:
 , ,  , , 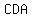 and and 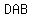
Let's take  : :
 side of this triangle is the side of this triangle is the 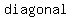 of the rectangle of the rectangle
 and and  are two sides of the rectangle, which potentially may be of different length (but we will prove they must be the are two sides of the rectangle, which potentially may be of different length (but we will prove they must be the 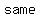 if the area of the inscribed rectangle is maximized). if the area of the inscribed rectangle is maximized).
The angle at  is the right angle since it is one of the angles of the rectangle, which by definition has four right angles. is the right angle since it is one of the angles of the rectangle, which by definition has four right angles.
Hence, looking at the triangle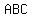 , we can see that this is a , we can see that this is a 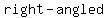 triangle inscribed in the circle. triangle inscribed in the circle.
Therefore to prove (1), we need to show that side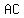 of any such triangle must be a diameter of circle. of any such triangle must be a diameter of circle.
Proof:
Choose any three points  , ,  and and  on the circle and connect these points to make a triangle on the circle and connect these points to make a triangle  . .
Let's suppose that the claim is that the angle at  is right angle. is right angle.
We will show that if this is true then it must follow that  is a is a 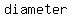 of the of the 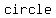 . .
Connect the center of the circle ( ) with each of the vertices of the triangle creating the segments ) with each of the vertices of the triangle creating the segments  , , 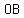 and and 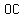 . .
Let's call the angle defined by the path 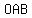 as as  and the angle defined by the path and the angle defined by the path 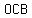 as as  . .
Since  , , 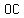 and and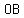 are all of are all of  length (equal to the length of the radius of the circle ) then length (equal to the length of the radius of the circle ) then  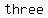 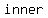  ( ( , ,  and and  ) are ) are 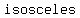 . .
We will next want to find the angle between  and and 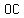 (the angle at (the angle at  made out by segments made out by segments  and and 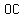 ) using only angles ) using only angles  and and  as given. as given.
The angle between  and and 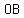 is equal to is equal to 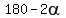 ° (due to the fact that ° (due to the fact that 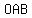 is is 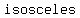 and the fact that the sum of all three internal angles in a triangle sum to and the fact that the sum of all three internal angles in a triangle sum to  °). °).
Similarly, the angle between 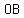 and and 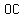 is equal to is equal to 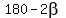 °. °.
Finally, since all the three angles at  add up to add up to  ° (full circle), it follows that the angle between ° (full circle), it follows that the angle between  and and 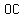 is equal to is equal to  . .
However, the angle at  of the original triangle of the original triangle  is equal to is equal to 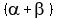 (follows from the fact that (follows from the fact that 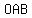 and and 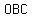 triangles are triangles are 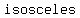 ). ).
This angle was claimed to be  ° and therefore the angle between ° and therefore the angle between  and and 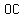 is equal to is equal to  °. °.
This means that the points  and and  and the and the 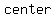 of the circle ( of the circle ( ) are ) are  . .
In other words, the 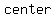 of the circle is of the circle is  on the straight line segment on the straight line segment  , which in turn means that , which in turn means that  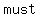 be a be a 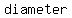 of the of the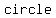 . .
So, we can conclude that  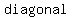 of the rectangle inscribed in a circle of the rectangle inscribed in a circle 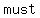 be a circles be a circles 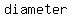 . .
|
|
|