SOLUTION: How many line segments can be drawn between 12 noncollinear points?

Algebra ->  Points-lines-and-rays -> SOLUTION: How many line segments can be drawn between 12 noncollinear points?      Log On


   

Question 622522: How many line segments can be drawn between 12 noncollinear points?
Answer by Edwin McCravy(20065) About Me  (Show Source):
You can put this solution on YOUR website!
How many line segments can be drawn between 12 noncollinear points?
Suppose those 12 noncollinear points are labeled
A,B,C,D,E,F,G,H,I,J,K,L. Then every possible combination of 2 letters from that set
of 12 indicates a different line segment.  So
the answer is 

The number of combinations of 12 things taken 2 at a time, aka

12 Choose 2

 or aka 

12C2 

 or aka

C(12,2)

which is calculated 

%2812%2A11%29%2F%282%2A1%29 

or 

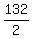132%2F2 

or 

66.  Here are all 66 line segments listed below.

 1.  AB
 2.  AC
 3.  AD
 4.  AE
 5.  AF
 6.  AG
 7.  AH
 8.  AI
 9.  AJ
10.  AK
11.  AL
12.  BC
13.  BD
14.  BE
15.  BF
16.  BG
17.  BH
18.  BI
19.  BJ
20.  BK
21.  BL
22.  CD
23.  CE
24.  CF
25.  CG
26.  CH
27.  CI
28.  CJ
29.  CK
30.  CL
31.  DE
32.  DF
33.  DG
34.  DH
35.  DI
36.  DJ
37.  DK
38.  DL
39.  EF
40.  EG
41.  EH
42.  EI
43.  EJ
44.  EK
45.  EL
46.  FG
47.  FH
48.  FI
49.  FJ
50.  FK
51.  FL
52.  GH
53.  GI
54.  GJ
55.  GK
56.  GL
57.  HI
58.  HJ
59.  HK
60.  HL
61.  IJ
62.  IK
63.  IL
64.  JK
65.  JL
66.  KL
 
Edwin