SOLUTION: Consider the line segment in the xy-plane whose left endpoint has coordinates (-1,0) and whose right end point has coordinates (3,0). Let this segment be divided into 1000 congruen

Algebra ->  Points-lines-and-rays -> SOLUTION: Consider the line segment in the xy-plane whose left endpoint has coordinates (-1,0) and whose right end point has coordinates (3,0). Let this segment be divided into 1000 congruen      Log On


   

Question 577803: Consider the line segment in the xy-plane whose left endpoint has coordinates (-1,0) and whose right end point has coordinates (3,0). Let this segment be divided into 1000 congruent segments, with points of division marked p1, p2,……, p999, going from left to right. What are the coordinates of p60?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The length of the segment is the distance between the ends of the segment.
The distance between the ends of the segment is the difference in x coordinates, because the y coordinates are the same. It's
3-%28-1%29=4
That segment is divided into 1000 congruent segments of length
4%2F1000=0.004
As the points are labeled p1 through p999 from left to right, from (-1,0) to 3,0), the coordinates for p1 will be
(-1+0.004,0) or (-0.996,0)
The coordinates for p2 will be
(-1+2(0.004),0) or (-0.992,0) and so on.
In general the x-coordinate for pn would be
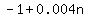
-1%2B0.004n
The y coordinate for all points in the segment is, of course, 0.
For p60, the x coordinate is
-1%2B0.004%2A60=-1%2B0.24=-0.76.
So, p60 is (-0.76,0).