Question 539220: Given the circle (x - 6)2 + (y + 2)2 = 9, determine if the line with an equation of 3x - 2y = 12 is a tangent to the circle, a secant to the circle, or neither.
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the circle (x - 6)2 + (y + 2)2 = 9, determine if the line with an equation of 3x - 2y = 12 is a tangent to the circle, a secant to the circle, or neither.
Let's see what we believe the answer is by looking at the graph. Then we'll show it by algebra.
 Judging by the graph it looks as though the line cuts through the
circle in two points, so it's probably a secant line, unless my
graph is off.
We will solve the system to see how many points of intersection there is.
There could be none, one or two.
(1) (x - 6)² + (y + 2)² = 9
(2) 3x - 2y = 12
We multiply the first equation out and simplify:
(1) (x - 6)(x - 6) + (y + 2)(y + 2) = 9
(3) x² - 12x + 36 + y² + 4y + 4 = 9
We solve (2) for y
(2) 3x - 2y = 12
-2y = -3x + 12
Judging by the graph it looks as though the line cuts through the
circle in two points, so it's probably a secant line, unless my
graph is off.
We will solve the system to see how many points of intersection there is.
There could be none, one or two.
(1) (x - 6)² + (y + 2)² = 9
(2) 3x - 2y = 12
We multiply the first equation out and simplify:
(1) (x - 6)(x - 6) + (y + 2)(y + 2) = 9
(3) x² - 12x + 36 + y² + 4y + 4 = 9
We solve (2) for y
(2) 3x - 2y = 12
-2y = -3x + 12
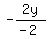 = = 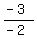 x + x +  y =
y =  x - 6
Substitute in (3)
(3) x² - 12x + 36 + y² + 4y + 4 = 9
x² - 12x + 36 + ( x - 6
Substitute in (3)
(3) x² - 12x + 36 + y² + 4y + 4 = 9
x² - 12x + 36 + ( x - 6)² + 4( x - 6)² + 4( x - 6) + 4 = 9
x² - 12x + 36 + ( x - 6) + 4 = 9
x² - 12x + 36 + ( x - 6)( x - 6)( x - 6) + 6x - 24 + 4 = 9
x² - 6x + 16 + ( x - 6) + 6x - 24 + 4 = 9
x² - 6x + 16 + ( x² - 9x - 9x + 36) = 9
x² - 6x + 16 + x² - 9x - 9x + 36) = 9
x² - 6x + 16 +  x² - 9x - 9x + 36 = 9
x² - 24x + 52 + x² - 9x - 9x + 36 = 9
x² - 24x + 52 +  x² = 9
Multiply through by 4 to clear of fractions:
4x² - 96x + 208 + 9x² = 36
13x² - 96x + 208 = 36
13x² - 96x + 172 = 0
We could solve that for x, they find y, but you weren't told to find
the solution, just to determine whether it was a secant line. So we
just need to show that that equation has two real solurtions:
The discriminant is b²-4ac = (-96)² - 4(13)(172) = 9216 - 8944 = 272
That is positive. Therefore there are two REAL solutions for x.
Therefore there are two points of intersection with the circle. So
it is a secant line.
You can go on and use the quadratic formula to find the two points of
intersection, but it isn't necessary. They are, however:
(x,y) = ( x² = 9
Multiply through by 4 to clear of fractions:
4x² - 96x + 208 + 9x² = 36
13x² - 96x + 208 = 36
13x² - 96x + 172 = 0
We could solve that for x, they find y, but you weren't told to find
the solution, just to determine whether it was a secant line. So we
just need to show that that equation has two real solurtions:
The discriminant is b²-4ac = (-96)² - 4(13)(172) = 9216 - 8944 = 272
That is positive. Therefore there are two REAL solutions for x.
Therefore there are two points of intersection with the circle. So
it is a secant line.
You can go on and use the quadratic formula to find the two points of
intersection, but it isn't necessary. They are, however:
(x,y) = ( , , 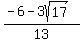 )
and
(x,y) = ( )
and
(x,y) = (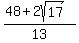 , , 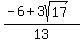 )
Edwin )
Edwin
|
|
|