Question 478813: My question is: Find the standard form of the equation for a circle with center (3, − 1) and solution point (−5, 1) .
Can you please explain how to solve it for future reference :). Thank You
Found 2 solutions by mananth, ewatrrr:
Answer by mananth(16946)   (Show Source):
Answer by ewatrrr(24785)  (Show Source):
You can put this solution on YOUR website!
Hi,
circle with center (3,-1)and solution point (-5,1)
r is the distance from the Center(3,-1) to the point on the circle (-5,1)
D =  =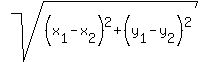 
Conics in general:
Standard Form of an Equation of a Circle is 
where Pt(h,k) is the center and r is the radius
Standard Form of an Equation of an Ellipse is 
where Pt(h,k) is the center and a and b are the respective vertices distances from center.
Standard Form of an Equation of an Hyperbola opening right and left is:
 where Pt(h,k) is a center with vertices 'a' units right and left of center.
Standard Form of an Equation of an Hyperbola opening up and down is:
 where Pt(h,k) is a center with vertices 'b' units up and down from center.
the vertex form of a parabola opening up or down,  where(h,k) is the vertex.
The standard form is  , where the focus is (h,k + p)
the vertex form of a parabola opening right or left,  where(h,k) is the vertex.
The standard form is  , where the focus is (h +p,k )
|
|
|
