SOLUTION: two circles of same dimensions pass through center of each other. what will be the area which is common to both circles in terms of area of any of the circles?if the radius of circ

 We want the football-shaped area in red below:


 

Draw a line segment connecting their centers, 
and line segments from the centers to their upper 
point of intersection:
 

 
That green triangle is an equilateral triangle because all its 
sides are radii of one circle or the other.
 
Therefore the angle marked is 60°, and all the green sides of
the equilateral triangle are "r" in length.
 
Now let's draw another equilateral triangle underneath it:


 
Those two 60° angles make a big 120° angle, so let's erase 
three of those green lines and mark that big angle 120°.



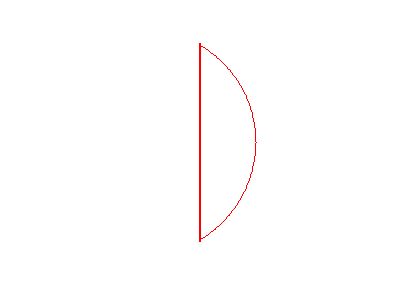
Now we'll lake away everything but the  (D-shaped) 
segment outlined in red, and leave the two green radii 
which make up the central angle of 120° which subtends 
the (D-shaped) segment outlined in red.

 

The formula for the area of a (D-shaped) sector of a circle is



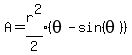where the subtending central angle is measured in radians.

We convert 120° to radians:   and substitute in the formula:


 



That's the area of this (D-shaped) segment, which is half of the 
desired area:



So the desired area of the entire overlapping part




is twice the area of the (D-shaped) sector or



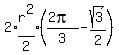or



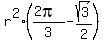Edwin