Question 452991: Points A, B, C, and D, lie on a circle. If the ratio of the arcs determined by these points are AB:BC= 2:4; BC:DC= 4:3; CD:DA= 1:2; then how many degrees are in each of the 4 arcs?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Points A, B, C, and D, lie on a circle.
If the ratio of the arcs determined by these points are:
AB:BC= 2:4;
BC:DC= 4:3;
CD:DA= 1:2;
then how many degrees are in each of the 4 arcs?
Let x = the multiplier
then
AB = 2x
BC = 4x
DC = 3x
Given: DC:DA, 1:2, replace DC with 3x, so we have
DA = 2(3x) = 6x
:
The 4 arcs add up to 360
2x + 4x + 3x + 6x = 360
15x = 360
x = 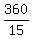
x = 24 is the multiplier
:
The arc values
AB = 2(24) 48 degrees
BC = 4(24) 96 degrees
DC = 3(24) 72 degrees
DA = 6(24)144 degrees
----------------------
total ck: 360 degrees
|
|
|