Question 439802: Hi! I need help on a problem my teacher gave me for homework.
On the problem, it gives me the lengths of two parallel chords in a circle. The lengths are 16 and 30. The distance between these chords is 23. How can I find the radius of this circle?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! the lengths of two parallel chords in a circle.
The lengths are 16 and 30.
The distance between these chords is 23.
How can I find the radius of this circle?
:
This will be easily understood if you roughly draw this out. We don't need to
draw a circle. We will solve this using right triangles
:
This is the way I pictured it
Draw the chords horizontally, the shorter (16) one above the longer one
Join the half way points of the chords, this line is 23 units, the center will fall on this line.
Mark the center closer to the longer chord
The radii run from the center to the ends of each chord and form the the hypotenuse of the right triangles.
:
We will find the distance each chord is from the center.
let x = distance from the longer chord to the center
then
(23-x) = distance from the shorter chord to the center
let r = the radius and will be the hypotenuse of the triangles
:
Two pythag equations
:
Short chord triangle
8^2 + (23-x)^2 = r^2
64 + 529 - 46x + x^2 = r^2
593 - 46x + x^2 = r^2
and
Long chord triangle
15^2 + x^2 = r^2
225 + x^2 = r^2
:
Since they both = r^2, we can write it
225 + x^2 = 593 - 46x + x^2
Subtract x^2 from both sides, solve for x
46x = 593 - 225
46x = 368
x = 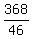
x = 8, is the distance the longer chord is from the center
and
23-8 = 15, is the distance the shorter chord is from the center
:
Solve for r (hypotenuse) of one of the equation
r^2 = 8^2 + 15^2
r^2 = 64 + 225
r^2 = 289
r = 
r = 17 is the radius of the circle
:
note that r will be the same from either triangle.
:
:
I tried to explain this so it would make sense to you.
I would appreciate it, if you would let me know, if I succeeded. C
|
|
|