|
Question 43222This question is from textbook algebra and trigonometry with analytic geometry
: find the point on the positive y-axis that is a distance 5 from the point P(3,4). I plotted it out to be B(0,8) But I'm not sure if this is right. Thanks for looking it over.
This question is from textbook algebra and trigonometry with analytic geometry
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! CONSTRUCTIONAL METHOD:
First locate the point P(3,4) on a graph paper.
Then draw a circle with centre at (3,4) and radius equal to 5 units.
This circle intersects the y-axis at two points A and B.
Find out the coordinates of these points from the graph.
You shall find coordinates of A and B are (0,8) and (0,0) respectively.

Both points A and B lies on y-axis and are at a distance of 5 units from P but only A lies on the positive y-axis. So the required point is A and the coordinates are (0,8).
ALTERNATIVE METHOD:
The distance 'd' between two points ( , , ) and ( ) and ( , , ) is given ) is given
 ____________(1) ____________(1)
In this problem let the coordinates of A and B are ( , , ) and ( ) and ( , , ) respectively. ) respectively.
Here,  = 5, = 5,  = 3, = 3,  = 4, = 4,  = 0 and = 0 and  = ? = ?
[Note  because the point ( because the point ( , , ) has to lie on y-axis] ) has to lie on y-axis]
Putting these values in (1) we have

Squaring both sides

or 
or 
or 
or 
or 
or 
Hence either 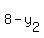 = 0 i.e. = 0 i.e.  = 8 or = 8 or  = 0. = 0.
As the reqd. point must be on positive y-axis, so  is the only possibility. is the only possibility.
Thus the coordinates of the point A which lie on positive y-axis and is at a distance of 5 units from (3,4) are (0,8).
|
|
|
| |