Question 412610: please help:
Let a, b, c, d be four points on a ciricle. Let four more circles pass through a and b, b and c, c and d, d and a, respectively, meeting in further points a'b'c'd'. Show that a'b'c'd' is a cyclic quadrilateral
Thank You!
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! I was able to solve this problem entirely by angle chasing. However, drawing a diagram on this website is extremely difficult, so I'll try to be as verbose as possible (maybe another tutor will post a diagram). I recommend you draw a diagram on your paper, going step by step carefully.
Since ABCD are four points on a circle, then ABCD is cyclic. Suppose that:
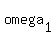 is the circle determined by A, B, A', B'. is the circle determined by A, B, A', B'.
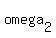 is the circle determined by B, C, B', C'. is the circle determined by B, C, B', C'.
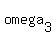 is the circle determined by C, D, C', D'. is the circle determined by C, D, C', D'.
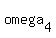 is the circle determined by D, A, D', A'. is the circle determined by D, A, D', A'.
Suppose that angle ADD' =  , angle D'DC = , angle D'DC =  , angle CBB' = , angle CBB' =  , and angle ABB' = , and angle ABB' =  . Since ABCD is cyclic, then . Since ABCD is cyclic, then  . Also, note that quadrilaterals ABB'A', BCC'B', CDD'C', and DAA'D' are all cyclic, as they are inscribed by circles . Also, note that quadrilaterals ABB'A', BCC'B', CDD'C', and DAA'D' are all cyclic, as they are inscribed by circles 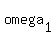 , ..., , ..., 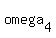 , so: , so:
angle AA'D' = 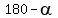
angle D'C'C = 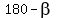
angle B'C'C = 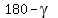
angle B'A'A = 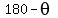
Hence, we can find that angle B'C'D' =  and angle B'A'D' = and angle B'A'D' =  . Since . Since  , then angle B'C'D' + angle B'A'D' = 180. They are opposite angles, so by definition, A'B'C'D' is cyclic. , then angle B'C'D' + angle B'A'D' = 180. They are opposite angles, so by definition, A'B'C'D' is cyclic.
|
|
|