SOLUTION: Write the standard form of the equation of the circle whose diameter has endpoints of (3, 0) and (7, 10)?

Algebra ->  Circles -> SOLUTION: Write the standard form of the equation of the circle whose diameter has endpoints of (3, 0) and (7, 10)?       Log On


   

Question 409204: Write the standard form of the equation of the circle whose diameter has endpoints of (3, 0) and (7, 10)?
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi

circle whose diameter has endpoints of (3, 0) and (7, 10)

(3, 0) and 

(7, 10) Midpoint is   (5,5)             |  ( %28x%5B1%5D+%2B+x%5B2%5D%29%2F2, %28y%5B1%5D+%2B+y%5B2%5D%29%2F2++%29)

(3, 0) and 

(7, 10  D = sqrt( (-4)^2 + (-10)^2))        |  D = 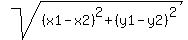sqrt+%28%28x1-x2%29%5E2%2B%28y1-y2%29%5E2%29%29 

  D = sqrt(116) = 2sqrt(29) and r = sqrt(29)

 Standard Form of an Equation of a Circle is %28x-h%29%5E2+%2B+%28y-k%29%5E2+=+r%5E2



where Pt(h,k) is the center and r is the radius

   (x-5)^2 + (y-5)^2 = 29