Question 407869: TWO PARALLEL CHORDS PQ AND MN ARE 3 cm APART ON THE SAME SIDE OF THE CIRCLE WHERE PQ=7 cm and MN = 14cm. CALCULATE THE RADIUS OF THE CIRCLE
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  and and  be the parallel chords with be the parallel chords with  as as 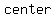 of the circle of the circle
given:
 and and  with distance with distance 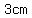 between the parallel chords between the parallel chords  and and  . .
Let  and and  be the be the  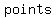 of of  and and  . .
Then 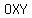 is a is a  line which is the line which is the 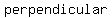 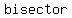 to both to both  and and 
This is the theorem of the line joining the center of the circle and the mid point of the chord is perpendicular to the chord .
Or else, a line joining the center of the circle cuts chord perpendicularly, then it bisects the chord.
So,  and and 
 ..........given ..........given
 and and 
Let  , ,
now from the right angled triangle, 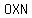 , by Pythagoras theorem, , by Pythagoras theorem,
 , where , where  is the is the 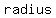 of the circle, of the circle,
or
 .........................(1) .........................(1)
Similarly from right triangle  , ,
 or or
 ...................(2). ...................(2).
From (1) and (2), left sides must be equal because right sides are equal:
 .solve for .solve for 



 . .
Therefore, from(1).


 is the radius of the circle. is the radius of the circle.
|
|
|