Question 389910: In circle P (P is center) , if BP=60 degrees, what is the length of BC? Round to the nearest tenth. Note: On my homework, it shows a picture of the circle. I can not show it to you, but here is the describtion: Line AC is a diameter, it is diagonal, C is at the upper right and A is at the lower left. From P, BP is a radius, it is vertical and on top of P. On the contrary, DP is another radius shown, and is horrizontal to the right of P. I hope this helps! Sorry for the poor description.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! In circle P (P is center) , if BP=60 degrees, what is the length of BC?
Round to the nearest tenth.
Note: On my homework, it shows a picture of the circle.
Line AC is a diameter, it is diagonal, C is at the upper right and A is at the lower left.
From P, BP is a radius, it is vertical and on top of P.
On the contrary, DP is another radius shown, and is horizontal to the right of P.
:
I think I can sort this out but am puzzled by BP=60 degrees, perhaps you mean
the length of BP is 60 units of some kind, so the radius = 60
:
The way I see this. Angle BPD = 90 degrees, Angle BPC = 45 degrees
If this is not the case, ignore my solution, I don't know how this should look
:
BPC is an isocoles triangle the two equal angles PBC and PCB =  = 67.5 degrees = 67.5 degrees
Line BC is opposite 45 degrees, use the law of sines:
 = = 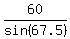
find the sines and Cross Multiply
.92388(BC) = .707*60
BC = 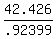
BC = 43.9
|
|
|