SOLUTION: Use the rational zero theorem to find all possible rational zeros for the polynomial function. m(x)= x^3+4x^2+4x+3

Algebra ->  Circles -> SOLUTION: Use the rational zero theorem to find all possible rational zeros for the polynomial function. m(x)= x^3+4x^2+4x+3      Log On


   

Question 388133: Use the rational zero theorem to find all possible rational zeros for the polynomial function. m(x)= x^3+4x^2+4x+3
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
Using the rational root theorem, the possible rational roots are -3, -1, 1, or 3. Now m(-1) = 2, m(1) = 12, m(3) = 78, but m(-3) = 0, so x = -3 is a (rational) root. By performing synthetic division, the quotient after dividing 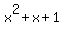m%28x%29=+x%5E3%2B4x%5E2%2B4x%2B3 by x + 3 is x%5E2+%2B+x+%2B+1, but the roots of this are complex, therefore -3 is the only rational root.