Question 331946: A circle is tangent to the y-axis and has a radius of 3 units.The center of the circle is in the third quadrant and lies on the graph of y - 2x = 0.What is the product of the coordinates (h, k) of the center of the circle?
Answer by galactus(183)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the conditions, we know that h=-3. That is, since the circle is tangent to the y-axis, lies in the third quadrant, and the radius is 3, the x-coordinate of the center must be at x=-3.
To find the y-coordinate, k, of the center use y=2x.
y=2(-3)=-6
The center coordinates are (-3,-6). The product is obviously (-6)(-3)=18.
The equation of the circle is 
To graph this on most calculators, we would have to solve this for y in terms of x.
If you have a graphing calculator, graph:
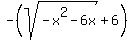 for the lower half of the circle for the lower half of the circle
and
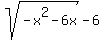 for the uppr half. for the uppr half.
Graph y=2x as well and you can see it pass through the center of the circle.
Casio calcualators have a nice Conics menu that graphs conics in terms of there equations without solving for y. It's a nice feature.
|
|
|