Question 280329: Dear Sir, Please help me!
ABCDEFGH is a regular octagon calculate ABC ACD ABD angles
Found 2 solutions by Alan3354, Theo:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! ABCDEFGH is a regular octagon calculate ABC ACD ABD angles
---------------------
Each interior angle is 135 degs
ABC = 135 degs
---------------
ACB = (180 - 135)/2 = 22.5 degs, so ACD = 135 - 22.5
ACD = 112.5 degs
---------------
ABD = ACD = 112.5 degs
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! ABCDEFGH is a regular octagon.
If so, then each interior angle is the same.
Each angle of an octagon can be found using the following general formula:
i = ((n-2)*180)/n where i = each interior angle and n = number of sides.
In a triangle, n = 3, and each interior angle would be 1*180/3 = 60 degrees.
In a rectangle, n = 4, and each interior angle would be 2*180/4 = 90 degrees.
In an octagon, n = 8, and each interior angle would be 6*180/8 = 1080/8 = 135 degrees.
Now your octagon is labeled ABCDEFGH.
You want to find the measure of:
ABC
ACD
ABD
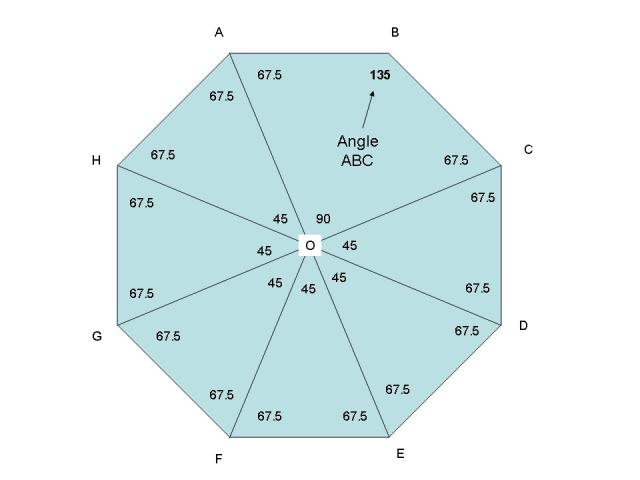
Angle ABC is one of the interior angles so angle ABC equals 135 degrees.
A picture of angle ABC is shown below:
Angle ACD = 112.5 degrees as shown in the following picture.
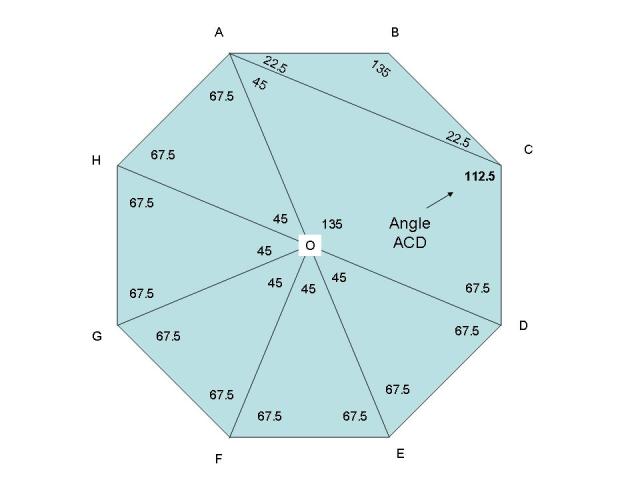
As you can see, Angle ACD creates a small triangle ABC. Since this is a regular polygon, then triangle ABC is an isosceles triangle. Since angle ABC is 135 degrees, the other 2 angles of the triangle have to be (180-135)/2 which equals 22.5 degrees. Since angle BCD is also equal to 135 degrees, and angle BCA is equal to 22.5 degrees, then angle ACD is equal to 135 minus 22.5 = 112.5 degrees.
Angle ABD = 112.5 degrees as shown in the following picture.
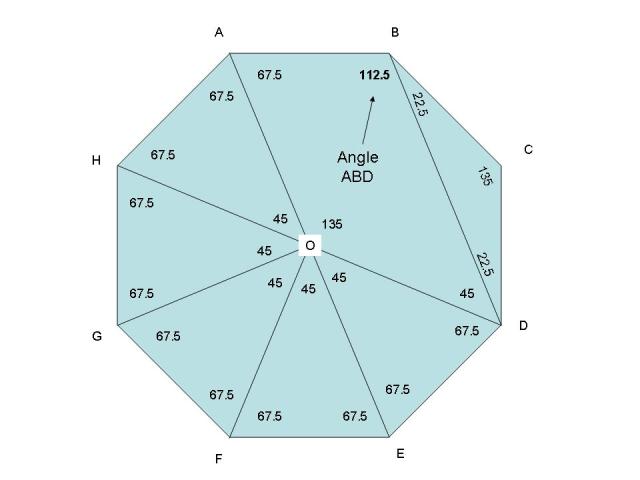
As you can see, Angle ABD creates a small triangle BCD. Since this is a regular polygon, then triangle BCD is an isosceles triangle. Since angle BCD is 135 degrees, the other 2 angles of the triangle have to be (180-135)/2 which equals 22.5 degrees. Since angle ABC is also equal to 135 degrees, and angle CBD is equal to 22.5 degrees, then angle ABD is equal to 135 minus 22.5 = 112.5 degrees.
|
|
|