You must get these in the standard form
for a circle
 Then the center is (h,k) and the radius is r.
A)
Then the center is (h,k) and the radius is r.
A)
 Get the constant term on the right by
adding
Get the constant term on the right by
adding 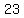 to both sides:
to both sides:
 Multiply the coefficient of
Multiply the coefficient of 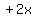 ,
which is
,
which is  by
by  , getting
, getting
 . Then square
. Then square  ,
getting
,
getting  and add
and add to
both sides, putting it right after the
to
both sides, putting it right after the
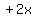 on the left:
on the left:
 Factor the first three terms on the left,
and combine the numbers on the right
Factor the first three terms on the left,
and combine the numbers on the right
 And write
And write 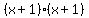 as
as 
 Multiply the coefficient of
Multiply the coefficient of 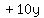 ,
which is
,
which is  by
by  , getting
, getting
 . Then square
. Then square  ,
getting
,
getting  and add
and add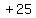 to
both sides, putting it right after the
to
both sides, putting it right after the
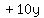 on the left:
on the left:
 Factor the last three terms on the left,
and combine the numbers on the right
Factor the last three terms on the left,
and combine the numbers on the right
 And write
And write 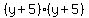 as
as 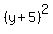
 and write
and write 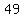 as
as 
 , which we compare to
, which we compare to
 , and so
since
, and so
since  then
then  , and
since
, and
since  then
then  , and
, and  so the center is (h,k) = (-1,-5) and the radius is r=7.
B)
so the center is (h,k) = (-1,-5) and the radius is r=7.
B)  Exactly the same way:
The constant term is already on the right,
so we don't have to get it over there.
Multiply the coefficient of
Exactly the same way:
The constant term is already on the right,
so we don't have to get it over there.
Multiply the coefficient of 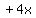 ,
which is
,
which is  by
by  , getting
, getting
 . Then square
. Then square  ,
getting
,
getting  and add
and add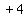 to
both sides, putting it right after the
to
both sides, putting it right after the
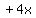 on the left:
on the left:
 Factor the first three terms on the left,
and combine the numbers on the right
Factor the first three terms on the left,
and combine the numbers on the right
 And write
And write  as
as 
 Multiply the coefficient of
Multiply the coefficient of 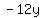 ,
which is
,
which is  by
by  , getting
, getting
 . Then square
. Then square  ,
getting
,
getting  and add
and add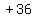 to
both sides, putting it right after the
to
both sides, putting it right after the
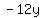 on the left:
on the left:
 Factor the last three terms on the left,
and combine the numbers on the right
Factor the last three terms on the left,
and combine the numbers on the right
 And write
And write 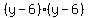 as
as 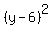
 and write
and write  as
as 
 , which we compare to
, which we compare to
 , and so
since
, and so
since  then
then  , and
since
, and
since  then
then  , and
, and  so the center is (h,k) = (-2,6) and the radius is r=8.
C)
so the center is (h,k) = (-2,6) and the radius is r=8.
C)  This is just like the other except it'e a little
easier because we don't have to complete the square
of y because there is no term in y, so we do something
else there. But we begin the same way:
This is just like the other except it'e a little
easier because we don't have to complete the square
of y because there is no term in y, so we do something
else there. But we begin the same way:
 Get the constant term on the right by
adding
Get the constant term on the right by
adding  to both sides:
to both sides:
 Multiply the coefficient of
Multiply the coefficient of 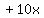 ,
which is
,
which is  by
by  , getting
, getting
 . Then square
. Then square  ,
getting
,
getting  and add
and add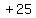 to
both sides, putting it right after the
to
both sides, putting it right after the
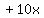 on the left:
on the left:
 Factor the first three terms on the left,
and combine the numbers on the right
Factor the first three terms on the left,
and combine the numbers on the right
 And write
And write 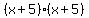 as
as 
 Now the only thing we have to do is write the
term
Now the only thing we have to do is write the
term  as
as 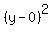
 Then write the 36 on the right as
Then write the 36 on the right as 
 , which we compare to
, which we compare to
 , and so
since
, and so
since  then
then  , and
since
, and
since  then
then  , and
, and  so the center is (h,k) = (5,0) and the radius is r=6.
Now be sure to learn how to do this by practicing on
some other problems like these, because even though I
can do your homework for you, I can't pass your tests
that you take in class for you, and your homework won't
do you any good if you flunk the tests, because your
teacher will then know you just got somebody to do your
homework for you.
Edwin
so the center is (h,k) = (5,0) and the radius is r=6.
Now be sure to learn how to do this by practicing on
some other problems like these, because even though I
can do your homework for you, I can't pass your tests
that you take in class for you, and your homework won't
do you any good if you flunk the tests, because your
teacher will then know you just got somebody to do your
homework for you.
Edwin