Question 265032: the points A (-4,0), B(4,8) and C(6,0) lie on a circle. the lines AB and BC are chords of the circle. find the coordinates of the centre of the circle. thank you so much if you could help!!
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! the solution is to find the equations of the
perpendicular bisectors of any 2 of the chords
formed by these 3 points.
The chords are:
AB
AC
BC
For the chord A(-4,0) to C(6,0):
The center of this chord is at P(1,0)
For the chord from B(4,8) to C(6,0):
The center of this chord is at P(5,4)
Now I have to find the slopes of these 2 chords
that I picked.
For the chord AC:
For the chord BC:
Now I need to find perpendicular bisectors of the chords
Any line perpendicular to AC will be parallel to the y-axis
since  is parallel to the x-axis.
And I also know the line goes through P(1,0).
This is just the line
(1) 
---------------------------------
Any line perpendicular to BC will have slope =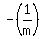 
And this line goes through P(5,4)
The formula to use is:
(2) 
----------------------------------
Now I just need to know where lines
(1) and (2) intersect
(1)
(2)
The 2 lines intersect at
the center of the circle at (1,3)
I'll try to plot line  to check
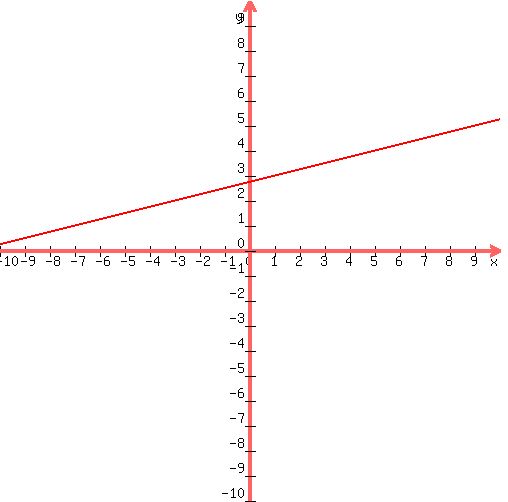
Looks like the line intersects at (1,3)
|
|
|
