Question 21445: At point P inside an equilateral triangle are connected to the vertices are 4, 5 and 6 respectively. Find the length of one side. all sides are equal sine it is equilateral.
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! I AM GIVING THE SOLUTION HERE ,BUT WOULD LIKE TO KNOW YOUR PRESENT COURSE OF STUDY AND YOUR PRESENT AWARENESS OF THE SUBJECT TO GIVE YOU A BETTER SOLUTION IF POSSIBLE
LET ABC BE THE EQUILATERAL TRIANGLE WITH SIDE=2A...LET P BE A POINT INSIDE THE TRIANGLE.JOIN PA,PB,PC.SINCE P IS INSIDE THE TRIANGLE WE CAN WRITE THAT
AREA.ABC =AREA.PBC+AREA.PCA+AREA.PAB
SINCE ABC IS EQUILATERAL TRIANGLE ITS AREA IS GIVEN BY SIDE*SIDE*SQ.RT3/4
=2A*2A*SQRT3/4=A*A*SQ.RT3
AREA OF A TRIANGLE IS GIVEN BY SQRT.OF{S(S-A)(S-B)(S-C)}WHERE S IS SEMIPERIMETER OF TRIANGLE{(A+B+C)/2},WITH A,B,C,AS ITS SIDES .
PBC HAS SIDES OF 2A,4,5
PCA HAS SIDES OF 2A,5,6
PAB HAS SIDES OF 2A,6,4
SO WITH THE ABOVE FORMULA WE GET
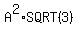 = = + +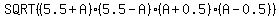 + +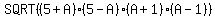
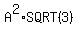 = = + + + +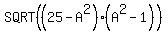
FROM THIS WE CAN SOLVE FOR A AND HENCE FIND THE SIDE OF THE TRIANGLE ...OFCOURSE IT IS A COMPLEX PROCESS..AND FOR YOU THE EASIEST WAY WOULD BE TO GO BY A GOAL SEEK TOOL USING XL IF YOU ARE FAMILIAR ..THE ANSWER IS THAT THE SIDE OF EQUILATERAL TRIANGLE =2A=8.5364
YOU CAN CHECK BY SUBSTITUTION IN THE ABOVE FOR MULA
|
|
|