|
Question 203604: Please someone help me about this :
Find the point of the intersection of the line y=x+2 and the circle (x-1)^2 + y^2=16
I guess i should find a point on the line which has distance 4 unit from the centre of the circle that is (1,o) but i don't know how!
Found 2 solutions by stanbon, Theo:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the point of the intersection of the line y=x+2 and the circle
(x-1)^2 + y^2=16
----------------
Substitute for "y" to get:
(x-1)^2 + (x+2)^2 = 16
x^2-2x+1 + x^2+4x+4 = 16
2x^2 +2x + 5 = 16
2x^2 + 2x - 9 = 0
--------------
x = [-2 +- sqrt(4 - 4*2*-9)]/4
x = [-2 +- sqrt(4 + 72)]/4
x = [-2 +- 2sqrt(19)]/4
-----------------
x = (-1/2) + (1/2)sqrt(19) or x = (-1/2)-(1/2)sqrt(19)
---------------
Substitute each of these into y = x+2 to get the y-values corresponding to the
x values:
Those y values will be (3/2)+(1/2)sqrt(19) and (3/2)-(1/2)sqrt(19)
=======================================================================
Cheers,
Stan H.
============================================
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your problem:
Find the point of the intersection of the line y=x+2 and the circle (x-1)^2 + y^2=16
I guess i should find a point on the line which has distance 4 unit from the centre of the circle that is (1,o) but i don't know how!
-----
It looks like you have 2 equations to deal with.
Equation 1 is 
Equation 2 is 
-----
In order to find the points of intersection, you need to find the values of x and y that satisfy both equations simultaneously.
-----
A relatively simple way to do this is to take the value of y in equation 1 and substitute it for the value of y in equation 2.
-----
equation 1 says that 
equation 2 says that 
if you substitute (x+2) for y in equation 2, you get:

-----
now you have one equation in one unknown that can be solved for x.
-----
since  and since and since  you substitute in equation: you substitute in equation:
 to get: to get:

when you combine like terms on the left side of this equation, you get:

-----
you can solve this by completing the square.
You could also solve this by using the quadratic formula.
We'll be solving it by completing the square.
-----
if you divide both sides of this equation by 2, you get:

-----
if you subtract 5/2 from both sides of this equation, you get:

-----
take ½ the b term which is the coefficient of x which is 1 and you get ½.
-----
Your squaring factor on the left side of the equation will be 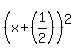
-----
when you multiply this squaring factor out you get:
-----

-----
since  then: then:

-----
Your equation had already become:

which can now become:

because 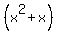 and and  are equivalent. are equivalent.
-----
your equation has now become:

If you add (1/4) to both sides of this equation, you get:

-----
if you take the square root of both sides of this equation, you get:
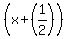 = +/- = +/- 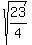
if you subtract (1/2) from both sides of this equation, you get:
 +/- +/- 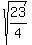
which makes x =:
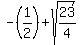
or
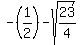
-----
This becomes:
-----
x = -2.8979
or
x = +1.8979
-----
We can use these values of x to solve for y.
-----
The equation of:
(x-1)^2 + y^2 = 16
becomes:
y = +/- 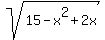
-----
This equation can also be used to graph the problem which will be shown below after all the algebra has been taken care of.
-----
if x = -2.8979, then y = +/- .897915762
-----
if x = 1.8979 then y = +/- 3.8979
-----
Of these possible values for y:
-----
y = -0.8979 satisfies both equations when x = -2.8979
-----
y = + 3.8979 satisfied both equations when x = +1.8979
-----
These look like your points of intersection of the line with the circle.
-----
The intersection points are represented by the ordered pair (x,y)
One point of intersection is (-2.8979,-0.8979)
The other point of intersection is (1.8979,3.8979)
A graph of the equation of the circle and a graph of the equation of the line are shown below and confirm the algebra.
-----

-----
|
|
|
| |